题目内容
15. 如图,⊙O的直径为10,弦AB=8,M是弦AB上的动点,则OM的长为整数时线段条数有( )
如图,⊙O的直径为10,弦AB=8,M是弦AB上的动点,则OM的长为整数时线段条数有( )| A. | 2条 | B. | 3条 | C. | 4条 | D. | 5条 |
分析 过点O作OC⊥AB于C,连接OA,根据垂径定理求出AC,根据勾股定理求出OC,求出OC的范围,即可得出选项.
解答 解:过点O作OC⊥AB于C,连接OA,
∵AB=8,
∴AC=BC=4,
∵半径OA=5,
∴OC=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴OM的长的范围是3≤OC≤5,
∴OM的长为整数时线段条数有3,4,4,5,5,共5条.
故选D.
点评 本题考查了垂径定理,勾股定理的应用,此题首先进行精确计算,求出OC和AC的长,然后进行逻辑推理,推断出符合要求的线段OC的条数即可.

练习册系列答案
相关题目
6.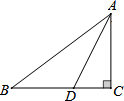 如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
 如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )| A. | ($\sqrt{2}$-1):1 | B. | ($\sqrt{2}$+1):1 | C. | $\sqrt{2}$:1 | D. | 2:1 |
20.下列各式中,没有意义的是( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{-3}$ | C. | $\sqrt{{{(-3)}^2}}$ | D. | $\root{3}{-1}$ |
4.某校春季运动会比赛中,八年级(1)班、(5)班的竞技实力相当,(1)班与(5)班得分比为6:5,(1)班得分比(5)班得分的2倍少40分,若设(1)班得x分,(5)班得y分,根据题意所列的方程组应为( )
| A. | $\left\{\begin{array}{l}{5x=6y}\\{x=2y-40}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x=6y}\\{x=2y+40}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{6x=5y}\\{x=2y+40}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6x=5y}\\{x=2y-40}\end{array}\right.$ |
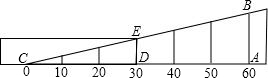 如图,测量小玻璃管口径的量具ABC中,AB的长是10毫米,AC被分成6等份,如果小管口DE正好对着量具上3份处(DE∥AB),那么小管口径DE的长是5毫米.
如图,测量小玻璃管口径的量具ABC中,AB的长是10毫米,AC被分成6等份,如果小管口DE正好对着量具上3份处(DE∥AB),那么小管口径DE的长是5毫米. 如图,∠1是Rt△ABC的一个外角,点D、E分别为边AB、AC的中点,∠1=110°,则∠2的度数是20°.
如图,∠1是Rt△ABC的一个外角,点D、E分别为边AB、AC的中点,∠1=110°,则∠2的度数是20°.