题目内容
17.已知函数y=(k-2)${x}^{3-{k}^{2}}$为反比例函数.(1)求k的值;
(2)它的图象在第二、四象限内,在各象限内,y随x增大而增大;
(3)当-3≤x≤-0.5时,此函数的最大值为8,最小值为$\frac{4}{3}$.
分析 (1)根据反比例函数的定义确定k的取值即可,注意比例系数不能为0;
(2)根据反比例函数的性质描述其图象的位置和增减性即可;
(3)根据反比例函数的增减性确定其最值即可.
解答 解:(1)∵y=(k-2)${x}^{3-{k}^{2}}$为反比例函数,
∴3-k2=-1,k-2≠0,
解得:k=-2;
(2)由(1)得反比例函数的解析式为y=-$\frac{4}{x}$,
∵k=-4<0,
∴它的图象在第二、四象限内,在各象限内,y随x增大而增大;
(3)∵当-3≤x≤-0.5,
∴$\frac{4}{3}$≤y≤8,
∴此函数的最大值为8,最小值为$\frac{4}{3}$.
点评 本题考查了反比例函数的性质及反比例函数的定义,能够利用反比例函数的定义求得其k的值是解答本题的关键,难度不大.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
7.2014年1月3日,国家发展改革委、住房城乡建设部出台“指导意见”,要求2015年底前,所有设市城市原则上全面实行居民阶梯水价制度.为了鼓励市民节约用水,嵊州市从2014年1月1日起实行居民生活用水按阶梯式水价计费.下表是居民“一户一表”生活用水阶梯式计费价格表的部分信息:
(注:到户价格=自来水价格+污水处理费,如:超过30吨的部分的到户价格=3.60+0.60=4.20(元),每户产生的污水量等于该户自来水用水量.)
若小王家2014年3月份用水25吨,交水费64.50元;2014年4月份用水30吨,交水费81.00元.
(1)求a,b;
(2)随着夏天的到来,用水量将增加.为了节省开支,小王家计划把2014年7月份的水费控制在家庭收入的1.5%.若小王的月收入为9600元,则小王家7月份用水多少吨?
| 自来水价格 | 污水处理费 | |
| 每户每月用水量 | 单价:元∕吨 | 单价:元∕吨 |
| 20吨及以下 | a | 0.60 |
| 超过20吨但不超过30吨的部分 | b | 0.60 |
| 超过30吨的部分 | 3.60 | 0.60 |
若小王家2014年3月份用水25吨,交水费64.50元;2014年4月份用水30吨,交水费81.00元.
(1)求a,b;
(2)随着夏天的到来,用水量将增加.为了节省开支,小王家计划把2014年7月份的水费控制在家庭收入的1.5%.若小王的月收入为9600元,则小王家7月份用水多少吨?
5.下列根式中,为最简二次根式的是( )
| A. | $\sqrt{\frac{1}{5}}$ | B. | $\sqrt{0.5}$ | C. | $\sqrt{5}$ | D. | $\sqrt{40}$ |
9.某红外线波长为0.00 000 094m,用科学记数法把0.00 000 094m可以写成( )
| A. | 9.4×10-7m | B. | 9.4×107m | C. | 9.4×10-8m | D. | 9.4×108m |
6.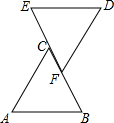 如图,已知EC=BF,∠A=∠D,现从下列6个条件:
如图,已知EC=BF,∠A=∠D,现从下列6个条件:
①AC=DF;②∠B=∠E;③∠ACB=∠DFE;④AB∥ED;⑤AB=ED;⑥DF∥AC;
从中选取一个条件,以保证△ABC≌△DEF,则可选择的是( )
 如图,已知EC=BF,∠A=∠D,现从下列6个条件:
如图,已知EC=BF,∠A=∠D,现从下列6个条件:①AC=DF;②∠B=∠E;③∠ACB=∠DFE;④AB∥ED;⑤AB=ED;⑥DF∥AC;
从中选取一个条件,以保证△ABC≌△DEF,则可选择的是( )
| A. | ②③④⑥ | B. | ③④⑤⑥ | C. | ①③④⑥ | D. | ①②③④ |
7.把二次函数y=-(x-2)2+6的图象向右平移2个单位,再向上平移3个单位,所得到图象的函数解析式是( )
| A. | y=-(x-4)2+9 | B. | y=-x2+9 | C. | y=-(x-5)2+8 | D. | y=-x2+8 |