题目内容
（1）分解因式：（a2+4）2-16a2
（2）解不等式组：
．
（2）解不等式组：
|
考点：解一元一次不等式组,因式分解-运用公式法
专题：
分析：（1）根据平方差公式把原式进行因式分解借口．
（2）分别求出各不等式的解集，再求出其公共解集即可．
（2）分别求出各不等式的解集，再求出其公共解集即可．
解答：解：（1）（a2+4）2-16a2
=（a2+4-4a）（a2+4+4a）
=（a-2）2（a+2）2；
（2）
，由①得，x≥-1，由②得，x＜2，
故此不等式组的解集为：-1≤x＜2．
=（a2+4-4a）（a2+4+4a）
=（a-2）2（a+2）2；
（2）
|
故此不等式组的解集为：-1≤x＜2．
点评：本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
一组数据：3，2，1，2，2的众数，中位数，极差分别是（ ）
| A、2，1，4 |
| B、2，2，2 |
| C、3，1，2 |
| D、2，1，2 |
美化城市，改善人们的居住环境已成为城市建设的一项重要内容，某市城区近几年来，通过拆迁旧房，植草，栽树，修建公园等措施，使城区绿地面积不断增加；
如图，在矩形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．求证：四边形EFGH是菱形．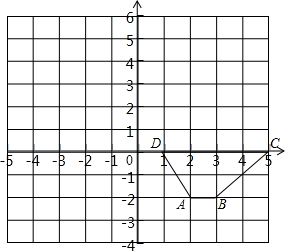
如图，在平面直角坐标系中，先把梯形ABCD向左平移6个单位长度得到梯形A1B1C1D1
如图，Rt△ABC中，∠ACB=90°，AC=3，BC=5，CD⊥AB，垂足为D，则∠DCB的正切值为
如图，AB∥CD，∠1=120°，∠2=56°，则∠3=