题目内容
3.解下列不等式(组),并把解集在数轴上表示出来(1)3(x-2)≥6-2(x+1)
(2)$\left\{\begin{array}{l}{x-3(x-2)≥4}\\{\frac{2x-1}{5}<\frac{x+1}{2}}\end{array}\right.$.
分析 (1)去括号,移项,合并同类项,系数化成1即可;
(2)先求出每个不等式的解集,再求出不等式组的解集即可.
解答 解:(1)3(x-2)≥6-2(x+1),
3x-6≥6-2x-2,
3x+2x≥6-2+6,
5x≥10,
x≥2,
在数轴上表示为: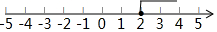 ;
;
(2)$\left\{\begin{array}{l}{x-3(x-2)≥4①}\\{\frac{2x-1}{5}<\frac{x+1}{2}②}\end{array}\right.$
∵解不等式①得:x≤1,
解不等式②得:x>-7,
∴不等式组的解集为-7<x≤1,
在数轴上表示为: .
.
点评 本题考查了解一元一次不等式(组),在数轴上表示不等式(组)的解集,能求出不等式或不等式组的解集是解此题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
14.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=4时,点R应运动到( )
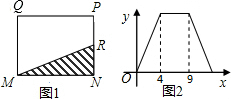

| A. | M处 | B. | N处 | C. | P处 | D. | Q处 |
15.甲、乙两个仓库要向A,B两地调运小麦,已知甲库可以调出80吨,乙库可以调出40吨,A地需要小麦50吨,B地需要70吨.甲,乙两库运往A,B两地的费用如下表:
(1)设甲库运往A地x吨,求总运费y(单位:元)与x之间的函数表达式;
(2)哪种方案总运费最省?并求最省的运费.
| A地(元/吨) | B地(元/吨) | |
| 甲库 | 10 | 40 |
| 乙库 | 20 | 30 |
(2)哪种方案总运费最省?并求最省的运费.
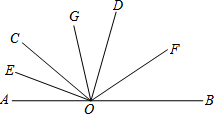 如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.将下列解题过程补充完整.
如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.将下列解题过程补充完整.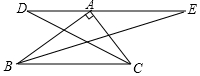 如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E,D,求DE的长.
如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E,D,求DE的长.