题目内容
 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连结AC,CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连结AC,CE.(1)求证:CD=CE;
(2)若AB=4,BC-AC=2,分别求弦BC、AE的长.
考点:圆周角定理,等腰三角形的判定与性质,勾股定理
专题:
分析:(1)根据圆周角定理由AB为⊙O的直径得∠ACB=90°,而DC=BC,根据等腰三角形的判定方法得到AB=AD,则∠D=∠B,由圆周角定理可得∠E=∠B,所以∠D=∠E,于是根据等腰三角形的判定即可得到CD=CE;
(2)在Rt△ACB中,利用勾股定理得到(BC-2)2+BC2=42,解得BC=1+
,则BD=2BC=2+2
,再证明△CDE∽△ADB,利用相似比可计算出DE=4+
,而AD=AB=4,所以AE=DE-AD=
.
(2)在Rt△ACB中,利用勾股定理得到(BC-2)2+BC2=42,解得BC=1+
| 7 |
| 7 |
| 7 |
| 7 |
解答:解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵DC=BC,
∴AB=AD,
∴∠D=∠B,
∵∠E=∠B,
∴∠D=∠E,
∴CD=CE;
(2)在Rt△ACB中,AB=4,BC-AC=2,即AC=BC-2,
∵AB2=AC2+BC2,
∴(BC-2)2+BC2=42,
整理得BC2-2BC-6=0,解得BC=1+
(BC=1-
舍去),
∴BD=2BC=2+2
,
∵∠D=∠D,∠B=∠E,
∴△CDE∽△ADB,
∴
=
,即DE=
=4+
,
∵AD=AB=4,
∴AE=DE-AD=4+
-4=
,
∴弦BC、AE的长分别为1+
,
.
∴∠ACB=90°,
∵DC=BC,
∴AB=AD,
∴∠D=∠B,
∵∠E=∠B,
∴∠D=∠E,
∴CD=CE;
(2)在Rt△ACB中,AB=4,BC-AC=2,即AC=BC-2,
∵AB2=AC2+BC2,
∴(BC-2)2+BC2=42,
整理得BC2-2BC-6=0,解得BC=1+
| 7 |
| 7 |
∴BD=2BC=2+2
| 7 |
∵∠D=∠D,∠B=∠E,
∴△CDE∽△ADB,
∴
| DE |
| DB |
| CD |
| AB |
(2+2
| ||||
| 4 |
| 7 |
∵AD=AB=4,
∴AE=DE-AD=4+
| 7 |
| 7 |
∴弦BC、AE的长分别为1+
| 7 |
| 7 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的判定与性质和勾股定理.

练习册系列答案
相关题目
 如图,数轴上有A、B、C、D四个点,其中表示互为相反数的点是( )
如图,数轴上有A、B、C、D四个点,其中表示互为相反数的点是( )| A、点A与点D |
| B、点A与点C |
| C、点B与点D |
| D、点B与点C |
 如图,ED∥AB,AF交ED于点C,∠1=138°,求∠A的度数.
如图,ED∥AB,AF交ED于点C,∠1=138°,求∠A的度数.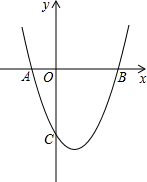 如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.