题目内容
(1)如图1,等边△ABC中,AB=2,点E是AB的中点,AD是高,P为AD上一点,则BP+PE的最小值等于______.
(2)如图2,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.

解:(1)作点E关于AD的对称点E',则E'在AC的中点处,连接BE',BE'与AD的交点即为点P的位置,

∵△ABC是等边三角形,
∴E'在AC的中点处,
∴BE⊥AC(三线合一),
又∵AB=2,
∴BE'= =
=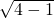 =
= ,
,
即BP+PE的最小值等于 .
.
(2)作点D关于AC的对称点D',连接D'B,并延长与AC的交点即为点P
 .
.
分析:(1)作点E关于AD的对称点E',则E'在AC的中点处,连接BE',BE'与AD的交点即为点P的位置,求出BE'的长度即可得出答案.
(2)作点D关于AC的对称点D',连接D'B,并延长与AC的交点即为点P.
点评:本题考查了轴对称求最短路径的问题及轴对称的性质,对于求最短路径的问题,我们可以作一个点关于直线的对称点,然后连接另一点与这个对称点,连线与直线的交点即为要求点的位置.

∵△ABC是等边三角形,
∴E'在AC的中点处,
∴BE⊥AC(三线合一),
又∵AB=2,
∴BE'=
 =
=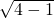 =
= ,
,即BP+PE的最小值等于
 .
.(2)作点D关于AC的对称点D',连接D'B,并延长与AC的交点即为点P
 .
.分析:(1)作点E关于AD的对称点E',则E'在AC的中点处,连接BE',BE'与AD的交点即为点P的位置,求出BE'的长度即可得出答案.
(2)作点D关于AC的对称点D',连接D'B,并延长与AC的交点即为点P.
点评:本题考查了轴对称求最短路径的问题及轴对称的性质,对于求最短路径的问题,我们可以作一个点关于直线的对称点,然后连接另一点与这个对称点,连线与直线的交点即为要求点的位置.

练习册系列答案
相关题目
 6、如图,在等边△ABC中,D、E分别是AB、AC的中点,DE=3,则△ABC的周长是( )
6、如图,在等边△ABC中,D、E分别是AB、AC的中点,DE=3,则△ABC的周长是( ) 12、如图,在等边△ABC中,AC=3,点O在AC上,且AO=1.点P是AB上一点,连接OP,以线段OP为一边作正△OPD,且O、P、D三点依次呈逆时针方向,当点D恰好落在边BC上时,则AP的长是
12、如图,在等边△ABC中,AC=3,点O在AC上,且AO=1.点P是AB上一点,连接OP,以线段OP为一边作正△OPD,且O、P、D三点依次呈逆时针方向,当点D恰好落在边BC上时,则AP的长是 9、如图,在等边三角形ABC中,三条中线AE,BD,CF相交于点O,则等边三角形ABC中,从△BOF到△COD需要经过的变换是( )
9、如图,在等边三角形ABC中,三条中线AE,BD,CF相交于点O,则等边三角形ABC中,从△BOF到△COD需要经过的变换是( )
 如图△AOB是等边三角形,点B的坐标为(4,0),则点A关于y轴的对称点A′的坐标为
如图△AOB是等边三角形,点B的坐标为(4,0),则点A关于y轴的对称点A′的坐标为