题目内容
在平面直角坐标系xOy中,设点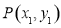 ,
,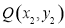 是图形W上的任意两点.
是图形W上的任意两点.
定义图形W的测度面积:若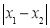 的最大值为m,
的最大值为m,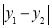 的最大值为n,则
的最大值为n,则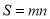 为图形W的测度面积.
为图形W的测度面积.
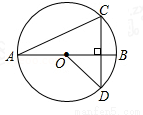
例如,若图形W是半径为1的⊙O.当P,Q分别是⊙O与x轴的交点时,如图1,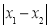 取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,
取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,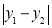 取得最大值,且最大值n=2.则图形W的测度面积
取得最大值,且最大值n=2.则图形W的测度面积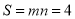 .
.
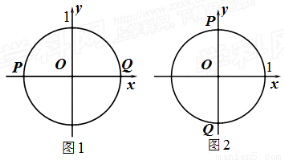
(1)若图形W是等腰直角三角形ABO,OA=OB=1.
①如图3,当点A,B在坐标轴上时,它的测度面积S= ;
②如图4,当AB⊥x轴时,它的测度面积S= ;
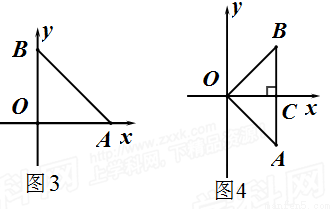
(2)若图形W是一个边长为1的正方形ABCD,则此图形测度面积S的最大值为 ;
(3)若图形W是一个边长分别为3和4的矩形ABCD,求它的测度面积S的取值范围.
(1)①1;②1;(2)2;(3) .
.
【解析】
试题分析:(1)①根据给出的定义可以求出来;
②根据给出的定义可以求出来;
(2)根据定义可以求出测度面积的最大值为2;
(3)因为平移图形W不会改变其测度面积S的大小,将矩形ABCD的其中一个顶点B平移至x轴上,注意分三种情况讨论,
试题解析:(1)① 1;
② 1.
(2) 2.
(3)不妨设矩形ABCD的边AB=4,BC=3.由已知可得,平移图形W不会改变其测度面积S的大小,将矩形ABCD的其中一个顶点B平移至x轴上.
当顶点A,B或B,C都在x轴上时,如图5和图6,矩形ABCD的测度面积S就是矩形ABCD的面积,此时S取得最小值,且最小值为12.
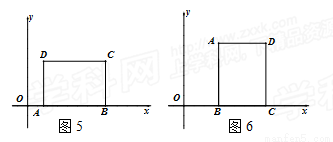
当顶点A,C都不在x轴上时,如图7.
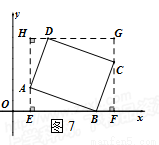
过A作直线AE⊥x轴于点E,过C作直线CF⊥x轴于点F,过D作直线GH∥x轴,与直线AE,CF分别交于点H和点G,则可得四边形EFGH是矩形.
当点P,Q分别与点A,C重合时,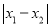 取得最大值
取得最大值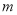 ,且最大值
,且最大值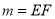 ;
;
当点P,Q分别与点B,D重合时,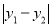 取得最大值
取得最大值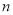 ,且最大值
,且最大值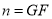 .
.
∴图形W的测度面积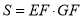 .
.
∵∠ABC=90°,∴∠ABE+∠CBF=90°,∵∠AEB=90°,∴∠ABE+∠BAE=90°,∴∠BAE=∠CBF.
又∵ ,∴△ABE∽△BCF,∴
,∴△ABE∽△BCF,∴ .
.
设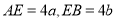
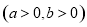 ,则
,则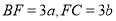 ,
,
在Rt△ABE中,由勾股定理得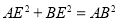 .
.
∴ .即
.即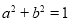 .∵
.∵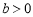 ,∴
,∴ ,易证△ABE≌△CDG.∴
,易证△ABE≌△CDG.∴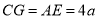 .∴
.∴ ,
,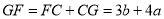 .
.
∴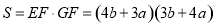
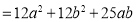
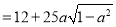
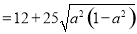
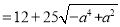

∴当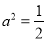 ,即
,即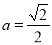 时,测度面积S取得最大值
时,测度面积S取得最大值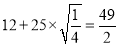 .
.
∵ ,∴
,∴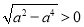 .∴
.∴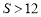 .
.
∴当顶点A,C都不在x轴上时,S的范围为 .
.
综上所述,测度面积S的取值范围是 .
.
考点:1.新定义;2.勾股定理.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
 ,则
,则 的值为( )
的值为( )  B.
B. C.
C. D.
D.
 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为 .
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为 .
 化为
化为 的形式,
的形式, ,
, 的值分别为( )
的值分别为( ) ,
, B.
B. ,
, C.
C. ,
, D.
D. ,
,

 .
. 于点B,联结PO并延长交
于点B,联结PO并延长交
 的切线;
的切线;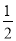 ,求
,求