题目内容
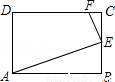
如图,PB切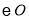 于点B,联结PO并延长交
于点B,联结PO并延长交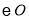 于点E,过点B作BA⊥PE交
于点E,过点B作BA⊥PE交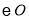 于点A,联结AP,AE.
于点A,联结AP,AE.

(1)求证:PA是 的切线;
的切线;
(2)如果OD=3,tan∠AEP=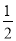 ,求
,求 的半径.
的半径.
(1)证明见试题解析;(2)5.
【解析】
试题分析:(1)连接OA、OB,根据垂径定理得出AB⊥OP,推出AP=BP,∠APO=∠BPO,证△PAO≌△PBO,推出∠PBO=∠PAO=90°,根据切线的判定推出即可;
(2)在Rt△ADE中,由tan∠AEP=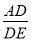 =
=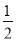 ,设AD=x,DE=2x,则OE=2x—3,在Rt△AOD中,由勾股定理,得
,设AD=x,DE=2x,则OE=2x—3,在Rt△AOD中,由勾股定理,得 .解出x,则可以求出⊙O的半径的长.
.解出x,则可以求出⊙O的半径的长.
试题解析:(1)证明:如图,联结OA,OB .∵PB是⊙O的切线,∴ ∠PBO=90°.∵ OA=OB,BA⊥PE于点D,∴ ∠POA=∠POB.又∵ PO=PO,∴ △PAO≌△PBO.∴ ∠PAO=∠PBO=90°.∴PA⊥OA.∴ 直线PA为⊙O的切线;

(2)在Rt△ADE中,∠ADE=90°,∵tan∠AEP=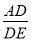 =
=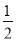 ,∴设AD=x,DE=2x,∴OE=2x—3,在Rt△AOD中,由勾股定理,得
,∴设AD=x,DE=2x,∴OE=2x—3,在Rt△AOD中,由勾股定理,得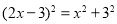 .解得,
.解得,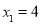 ,
,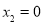 (不合题意,舍去).∴ AD=4,OA=OE=2x-3=5.即⊙O的半径的长5.
(不合题意,舍去).∴ AD=4,OA=OE=2x-3=5.即⊙O的半径的长5.
考点:切线的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
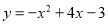 .(1)求出这个抛物线的对称轴和顶点坐标;(2)在给定的坐标系中画出这个抛物线,若抛物线与x轴交于A,B两点,与y轴交于点C,求△ABC的面积.
.(1)求出这个抛物线的对称轴和顶点坐标;(2)在给定的坐标系中画出这个抛物线,若抛物线与x轴交于A,B两点,与y轴交于点C,求△ABC的面积.
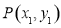 ,
,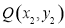 是图形W上的任意两点.
是图形W上的任意两点.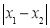 的最大值为m,
的最大值为m,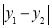 的最大值为n,则
的最大值为n,则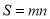 为图形W的测度面积.
为图形W的测度面积.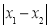 取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,
取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,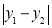 取得最大值,且最大值n=2.则图形W的测度面积
取得最大值,且最大值n=2.则图形W的测度面积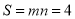 .
.
 B.
B. C.
C. D.
D.
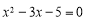 的根的情况是( )
的根的情况是( )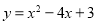 .
.
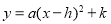 的形式;
的形式;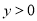 .
.

 ,则下列比例式成立的是 ( )
,则下列比例式成立的是 ( ) B.
B. C.
C. D.
D.