题目内容
4.问题背景:在正方形ABCD的外侧,作△ADE和△DCF,连结AF、BE.特例探究:如图①,若△ADE与△DCF均为等边三角形,试判断线段AF与BE的数量关系和位置关系,并说明理由;
拓展应用:如图②,在△ADE与△DCF中,AE=DF,ED=FC,且BE=4,则四边形ABFE的面积为8.
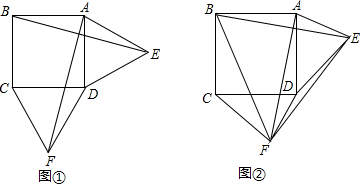
分析 特例探究:易证△ADE≌△DCF,即可证明AF与BE的数量关系是:AF=BE,位置关系是:AF⊥BE;
拓展应用:首先证得△ADE≌△CDF,由全等三角形的性质可得∠DAE=∠CDF,易得△BAE≌△ADF,可得AE=AF,同特例探究可得AF⊥BE,易得四边形ABFE的面积为:$\frac{1}{2}•AF•BE$.
解答 解:特例探究:AF=BE,AF⊥BE.
∵四边形ABCD为正方形,△ADE与△DCF均为等边三角形,
∴AB=AD=CD,∠BAD=∠ADC,AE=AD=CD=DF,∠DAE=∠CDF,
∴∠BAD+∠DAE=∠ADC+∠CDF,即∠BAE=∠ADF,
在△ABE与△DAF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠ADF}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△DAF(SAS),
∴AF=BE,∠ABE=∠DAF,
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴AF⊥BE;
拓展应用:在△ADE与△CDF中,
∵$\left\{\begin{array}{l}{AD=CD}\\{AE=DF}\\{CF=DE}\end{array}\right.$,
∴△ADE≌△CDF(SSS),
∴∠DAE=∠CDF,∠ADF=∠ADC+∠CDF=90°+∠CDF,∠BAE=∠BAD+∠EAD=90°+∠EAD,
∴∠ADF=∠BAE,
在△ABE与△DAF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠ADF}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△DAF(SAS),
∴AF=BE,∠ABE=∠DAF,
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴AF⊥BE,
∴S四边形ABFE=$\frac{1}{2}•AF•BE=\frac{1}{2}×4×4$=8,
故答案为:8.
点评 本题主要考查了正方形的性质和等边三角形的性质,证得AF=BE,AF⊥BE是解答此题的关键.

| A. | 2a2-4a2=-2 | B. | 3a+a=3a2 | C. | 5b•b=5b2 | D. | 4a6÷2a3=2a2 |
| A. | a6÷a3=a2 | B. | a3•a4=a7 | C. | (a2)3=a5 | D. | 2a3+a3=3a6 |
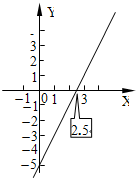 如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是
如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是( )
| A. | x>2.5 | B. | x<2.5 | C. | x>-5 | D. | x<-5 |
| A. | a3+a3=a6 | B. | a2•a2=a4 | C. | (2a)4=2a4 | D. | a6÷a3=a2 |
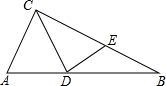 如图,在Rt△ABC中,∠C=90°,AC=3,将△ACD沿CD翻折,使点A落在BC的中点E处,则点D到BC的距离是2.
如图,在Rt△ABC中,∠C=90°,AC=3,将△ACD沿CD翻折,使点A落在BC的中点E处,则点D到BC的距离是2.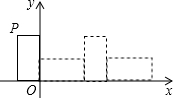 如图,把小矩形放在第二象限,使两条边与坐标轴重合,然后将小矩形无滑动的沿x轴顺时针滚动,每一次边落在x轴上记作一次操作,己知顶点P(-1,2),则经过2015次操作后点P的坐标为(3021,0).
如图,把小矩形放在第二象限,使两条边与坐标轴重合,然后将小矩形无滑动的沿x轴顺时针滚动,每一次边落在x轴上记作一次操作,己知顶点P(-1,2),则经过2015次操作后点P的坐标为(3021,0).