题目内容
17. 如图,在Rt△ABC与Rt△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE=30°,连接BD,CE,试确定BD和CE的数量关系,并说明理由.
如图,在Rt△ABC与Rt△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE=30°,连接BD,CE,试确定BD和CE的数量关系,并说明理由.
分析 根据三角形的内角和和直角三角形的性质得到∠EAD=∠CAB=60°,AD=2AE,AB=2AC,推出△EAD∽△CAB,得到$\frac{AE}{AD}=\frac{AC}{AB}$,于是得到△EAC∽△DAB,求得$\frac{BD}{CE}=\frac{AD}{AE}$=2,即可得到结论.
解答 解:BD=2CE,
理由:∵∠ACB=∠AED=90°,∠ABC=∠ADE=30°,
∴∠EAD=∠CAB=60°,AD=2AE,AB=2AC,
∴∠EAC=∠DAB,△EAD∽△CAB,
∴$\frac{AE}{AD}=\frac{AC}{AB}$,
∴△EAC∽△DAB,
∴$\frac{BD}{CE}=\frac{AD}{AE}$=2,
∴BD=2CE.
点评 本题考查了相似三角形的判定和性质,直角三角形的性质,熟练掌握直角三角形的性质是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
5.下列美丽的图案中,是中心对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.将一些半径相同的小圆按如图所示的规律摆放: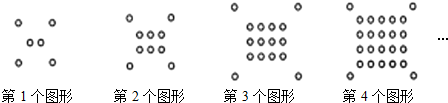
(1)填写下表:
(2)照这样的规律搭下去,搭第8个这样的图形需要76个小圆.

(1)填写下表:
| 图形序号 | 1 | 2 | 3 | 4 | 5 |
| 小圆个数 | 6 | 10 | 16 | 24 | 34 |
 已知△ABC中,BC=26cm,AB、AC的垂直平分线分别交BC于E、F,则△EAF周长26cm.
已知△ABC中,BC=26cm,AB、AC的垂直平分线分别交BC于E、F,则△EAF周长26cm. 某地区有一种植物在气温0℃以下持续时间超过2.5小时,即遭霜冻灾害,需采取预防措施,如图是气象台某天发布的该地区气象信息,预报了次日0时至5时气温随时间变化情况,气温是时间的二次函数,它的图象经过点(0,2),其顶点坐标是($\frac{5}{2}$,-$\frac{9}{8}$),请你根据图中信息判断这种植物次日是否需要采取防冻措施?并说明理由.
某地区有一种植物在气温0℃以下持续时间超过2.5小时,即遭霜冻灾害,需采取预防措施,如图是气象台某天发布的该地区气象信息,预报了次日0时至5时气温随时间变化情况,气温是时间的二次函数,它的图象经过点(0,2),其顶点坐标是($\frac{5}{2}$,-$\frac{9}{8}$),请你根据图中信息判断这种植物次日是否需要采取防冻措施?并说明理由. 已知实数a,b,c在数轴上所对应的点如图所示,完成下列各题.
已知实数a,b,c在数轴上所对应的点如图所示,完成下列各题. 如图,△ABC中,AD平分∠BAC,AD的垂直平分线FE交BC的延长线于E,求证:DE2=BE•CE.
如图,△ABC中,AD平分∠BAC,AD的垂直平分线FE交BC的延长线于E,求证:DE2=BE•CE. 已知:如图,在△ABC中,∠C=90°,AC=4,CB=5,D是BC边上一点,且DB=2,点E是AC边上的一个动点,过点E作EF∥CB交AD于点F.
已知:如图,在△ABC中,∠C=90°,AC=4,CB=5,D是BC边上一点,且DB=2,点E是AC边上的一个动点,过点E作EF∥CB交AD于点F.