题目内容
19. 如图所示的圆柱体中底面圆的半径是$\frac{3}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是3$\sqrt{2}$(结果保留根号).
如图所示的圆柱体中底面圆的半径是$\frac{3}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是3$\sqrt{2}$(结果保留根号).
分析 先将图形展开,再根据两点之间线段最短,由勾股定理可得出.
解答  解:圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,C是边的中点,矩形的宽即高等于圆柱的母线长.
解:圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,C是边的中点,矩形的宽即高等于圆柱的母线长.
∵AB=π•$\frac{3}{π}$=3,CB=3.
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 此题主要考查了平面展开图最短路径问题,此矩形的长等于圆柱底面周长,矩形的宽即高等于圆柱的母线长.本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
9.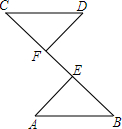 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )| A. | AE=DF | B. | ∠A=∠D | C. | ∠B=∠C | D. | AB=DC |
7.受地震的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从两养殖场调运鸡蛋到超市的路程和运费如表:
(1)若某天调运鸡蛋的总运费为2670元,则从甲、乙两养殖场各调运了多少斤鸡蛋?
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?
| 到超市的路程(千米) | 运费(元/斤•千米) | |
| 甲养殖场 | 200 | 0.012 |
| 乙养殖场 | 140 | 0.015 |
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?
14.已知$\sqrt{a+2}+|b-1|=0$,那么(a+b)2015的值为( )
| A. | -1 | B. | 1 | C. | 32007 | D. | -32007 |




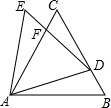 已知:D是等边△ABC中BC边上一个不与B,C重合的动点,且△ADE也是等边三角形.
已知:D是等边△ABC中BC边上一个不与B,C重合的动点,且△ADE也是等边三角形.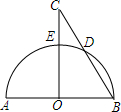 ⊙O直径AB长为6,CO⊥AB,CO=4,求:CD的长.
⊙O直径AB长为6,CO⊥AB,CO=4,求:CD的长.