题目内容
1.如果$\sqrt{a-b}$+(b-3)2=0,则$\sqrt{a+b}$的值为$\sqrt{6}$.分析 根据非负数的性质求得a、b的值,再代入求解可得.
解答 解:∵$\sqrt{a-b}$+(b-3)2=0,
∴a-b=0且b-3=0,
则a=b=3,
∴$\sqrt{a+b}$=$\sqrt{3+3}$=$\sqrt{6}$,
故答案为:$\sqrt{6}$.
点评 本题考查了非负数的性质:算术平方根、偶次方,几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
12.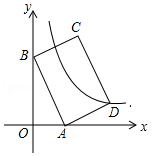 如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=$\frac{k}{x}$的图象经过点D,则k值为( )
如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=$\frac{k}{x}$的图象经过点D,则k值为( )
 如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=$\frac{k}{x}$的图象经过点D,则k值为( )
如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=$\frac{k}{x}$的图象经过点D,则k值为( )| A. | -14 | B. | 14 | C. | 7 | D. | -7 |
9.下面的数中,比0小的是( )
| A. | $\frac{1}{2016}$ | B. | 0.01 | C. | |-2016| | D. | -2016 |
16.一元二次方程x2+x+0.25=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定根的情况 |
6.已知相互垂直的直线l1:y=k1x+2-k1与l2:y=k2x+2-3k2交于点P,O为坐标原点,则OP的最大值是( )
| A. | $\sqrt{13}$ | B. | $\sqrt{3}+2$ | C. | 4$\sqrt{2}+9$ | D. | 2$\sqrt{2}+1$ |
11.下列从左到右的变形是因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | (a-b)(m-n)=(b-a)(n-m) | C. | ax-ay=a(x-y) | D. | m2-2m-3=m(m-2-$\frac{3}{m}$) |