题目内容
6.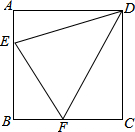 已知:如图,点E是正方形ABCD的边AB上一点,点F是边BC上一点,且AE+CF=EF.求∠EDF的度数.
已知:如图,点E是正方形ABCD的边AB上一点,点F是边BC上一点,且AE+CF=EF.求∠EDF的度数.
分析 先根据正方形的性质得DA=DC,∠ADC=90°,于是可把△DAE绕点D逆时针旋转90°得△DCG,如图,根据旋转的性质得CG=AE,DE=DG,∠DCG=∠A=90°,∠EDG=90°,则可判断点G在BC的延长线上和EF=GF,接着证明△DEF≌△DGF,根据全等三角形的性质得∠EDF=∠GDF,所以∠EDF=$\frac{1}{2}$∠EDG=45°.
解答 解:∵四边形ABCD为正方形,
∴DA=DC,∠ADC=90°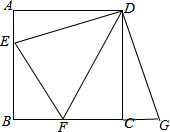 ∴把△DAE绕点D逆时针旋转90°可得△DCG,如图,
∴把△DAE绕点D逆时针旋转90°可得△DCG,如图,
∴CG=AE,DE=DG,∠DCG=∠A=90°,∠EDG=90°,
∴点G在BC的延长线上,
而AE+CF=EF,
∴CG+CF=EF,即EF=GF,
在△DEF和△DGF中
$\left\{\begin{array}{l}{DE=DG}\\{DF=DF}\\{EF=GF}\end{array}\right.$,
∴△DEF≌△DGF,
∴∠EDF=∠GDF,
∴∠EDF=$\frac{1}{2}$∠EDG=45°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和正方形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知平行四边形的一边长为10,则对角线的长度可能取下列数组中的( )
| A. | 4、8 | B. | 8、6 | C. | 8、10 | D. | 11、13 |
11.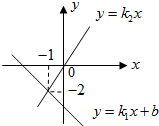 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
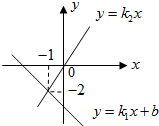 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )| A. | x>-1 | B. | x<-1 | C. | x<-2 | D. | 无法确定 |
15.点A关于原点对称的点的坐标是(3,-6),则点A的坐标是( )
| A. | (3,6) | B. | (-3,6) | C. | (3,-6) | D. | (-3,-6) |