题目内容
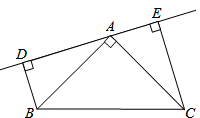 如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作经过点A的直线的垂线段BD,CE,若BD=3厘米,CE=4厘米,则DE的长为
如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作经过点A的直线的垂线段BD,CE,若BD=3厘米,CE=4厘米,则DE的长为考点:全等三角形的判定与性质
专题:计算题
分析:利用垂直的定义得到一对直角相等,由∠BAC=90°,利用平角的定义得到一对角互余,利用同角的余角相等得到一对角相等,再由AB=AC,利用AAS得到三角形ABD与三角形ACE全等,利用全等三角形对应边相等得到DB=AE=3厘米,AD=CE=4厘米,由DE=AD+AE即可求出DE长.
解答:解:∵BD⊥DE,CE⊥DE,BA⊥AC,
∴∠BDA=∠BAC=∠AEC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴DB=AE=3厘米,CE=AD=4厘米,
则DE=AD+AE=4+3=7厘米.
故答案为:7厘米.
∴∠BDA=∠BAC=∠AEC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴DB=AE=3厘米,CE=AD=4厘米,
则DE=AD+AE=4+3=7厘米.
故答案为:7厘米.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在Rt△ADB中,∠D=90°,C为AD上一点,若△CBD∽△BAD,则x的可能值是( )
如图,在Rt△ADB中,∠D=90°,C为AD上一点,若△CBD∽△BAD,则x的可能值是( )| A、15 | B、20 | C、25 | D、30 |
下列关于判断一个数学结论是否正确的叙述正确的是( )
| A、只需观察得出 |
| B、只需依靠经验获得 |
| C、通过亲自实验得出 |
| D、必须进行有根据地推理 |
 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②AP=BQ;③PQ∥AE;④∠AOB=60°;⑤DE=DP.
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②AP=BQ;③PQ∥AE;④∠AOB=60°;⑤DE=DP.