题目内容
16.实数$\frac{22}{7}$,$\sqrt{8}$,1.412,$\frac{2}{3}$π,$\sqrt{16}$,1.2020020002…,$\root{3}{27}$,2-$\sqrt{5}$中,无理数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 无理数就是无限不循环小数,根据定义即可判断.
解答 解:无理数有:$\sqrt{8}$,$\frac{2}{3}$π,1.2020020002…,2-$\sqrt{5}$共4个.
故选C.
点评 本题考查了无理数的定义,无理数常见的三种类型(1)开不尽的方根,如$\sqrt{2}$等.(2)特定结构的无限不循环小数,如0.303 003 000 300 003…(两个3之间依次多一个0).(3)含有π的绝大部分数,如2π.注意:判断一个数是否为无理数,不能只看形式,要看化简结果.如$\sqrt{16}$是有理数,而不是无理数.

练习册系列答案
相关题目
7.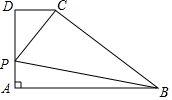 如图,四边形ABCD是直角梯形,AB∥CD,AD⊥AB,CD=3,AB=9,AD=5,点P是腰AD上的一个动点,要使PC+PB最小,其最小值为( )
如图,四边形ABCD是直角梯形,AB∥CD,AD⊥AB,CD=3,AB=9,AD=5,点P是腰AD上的一个动点,要使PC+PB最小,其最小值为( )
 如图,四边形ABCD是直角梯形,AB∥CD,AD⊥AB,CD=3,AB=9,AD=5,点P是腰AD上的一个动点,要使PC+PB最小,其最小值为( )
如图,四边形ABCD是直角梯形,AB∥CD,AD⊥AB,CD=3,AB=9,AD=5,点P是腰AD上的一个动点,要使PC+PB最小,其最小值为( )| A. | 13 | B. | $\sqrt{13}$ | C. | $\sqrt{82}$ | D. | $\sqrt{85}$ |
11.下列关于x的一元二次方程没有实数根的是( )
| A. | x2=3 | B. | x2=x | C. | x2+x+1=0 | D. | x2-x-1=0 |
1.大于-2.5,不小于2的整数共有( )个.
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
