题目内容
19.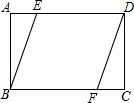 如图,在矩形ABCD中,AB=3,AD=4,点E、F分别在AD、BC上,连接BE、DF,若四边形BFDE是菱形,则S菱形BFDE=$\frac{75}{8}$.
如图,在矩形ABCD中,AB=3,AD=4,点E、F分别在AD、BC上,连接BE、DF,若四边形BFDE是菱形,则S菱形BFDE=$\frac{75}{8}$.
分析 设菱形的边长为x,则AE=AD-x,由菱形的性质可知BE=AD,在Rt△ABE中利用勾股定理可建立关于x的方程,解方程求出x的值,即可求出S菱形BFDE.
解答 解:
∵四边形ABCD是矩形,
∴∠A=90°,
∵四边形BFDE是菱形,
∴BE=DE,
菱形的边长为x,则AE=AD-x=4-x,
在Rt△ABE中,AB2+AE2=BE2,即32+(4-x)2=x2,
解得:x=$\frac{25}{8}$,
∴S菱形BFDE=AB•DE=$\frac{75}{8}$,
故答案为:$\frac{75}{8}$.
点评 本题考查了矩形的性质、菱形的性质以及勾股定理的运用,熟记特殊四边形的各种性质是解题关键.

练习册系列答案
相关题目
7.下列交通标志中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,是二元一次方程2x+ay=3的一个解,则a的值为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 1 | D. | -1 |
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等边三角形 | B. | 菱形 | C. | 等腰直角三角形 | D. | 平行四边形 |
11.一元一次方程$\frac{2x+1}{3}$-$\frac{x-3}{6}$=1,去分母后得( )
| A. | 2(2x+1)-x-3=1 | B. | 2(2x+1)-x-3=6 | C. | 2(2x+1)-(x-3)=1 | D. | 2(2x+1)-(x-3)=6 |
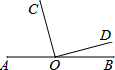 如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的度数是75°.
如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的度数是75°.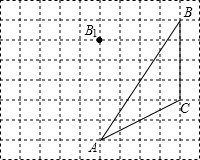 如图,方格纸中每个小正方形的边长为1cm,平移图中的△ABC,使点B移到点B1的位置.
如图,方格纸中每个小正方形的边长为1cm,平移图中的△ABC,使点B移到点B1的位置.