题目内容
3.(1)已知,32m=5,3n=10.求9m-n的值.(2)已知x2+x-2=5,求x4+x-4的值
(3)已知x2-5x+1=0,求$\frac{{x}^{4}+1}{{x}^{2}}$的值.
分析 (1)由已知等式求出9m=5,9n=100,原式利用同底数幂的除法法则变形,计算即可得到结果;
(2)已知等式两边平方,利用完全平方公式化简,即可求出所求式子的值;
(3)已知等式变形求出x+$\frac{1}{x}$的值,原式变形后代入计算即可求出值.
解答 解:(1)∵32m=5,3n=10,
∴9m=5,9n=100,
则9m-n=$\frac{9^m}{9^n}$=$\frac{1}{20}$;
(2)∵x2+x-2=5,
∴(x2+x-2)2=25,即x4+2+x-4=25,
则x4+x-4=23;
(3)∵x2-5x+1=0,x≠0,
∴x+$\frac{1}{x}$=5,
则原式=x2+$\frac{1}{x^2}$=(x+$\frac{1}{x}$)2-2=23.
点评 此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.下列语句是命题的是( )
| A. | 有公共顶点的两个角是对顶角 | B. | 在一条直线上任取一点O | ||
| C. | 过点O作直线MN的平行线 | D. | 过点O作直线MN的垂线 |
13.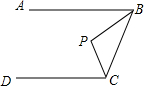 如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
 如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )| A. | 120° | B. | 90° | C. | 75° | D. | 60° |