题目内容
19.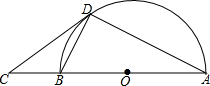 如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.
如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.(1)求证:∠BAD=∠BDC;
(2)若∠BDC=28°,BD=2,求⊙O的半径.(精确到0.01)
分析 (1)连接OD,利用切线的性质和直径的性质转化为角的关系进行证明即可;
(2)根据三角函数进行计算即可.
解答 证明:(1)连接OD,如图,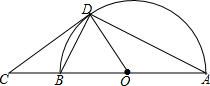
∵CD与半圆O相切于点D,
∴OD⊥CD,
∴∠CDO=90°,即∠CDB+∠BDO=90°,
∵AB是半圆O的直径,
∴∠ADB=90°,即∠ADO+∠BDO=90°,
∴∠CDB=∠ODA,
∵OD=OA,
∴∠ODA=∠BAD,
∴∠BAD=∠BDC;
(2)∵∠BAD=∠BDC=28°,在Rt△ABD中,sin∠BAD=$\frac{BD}{AB}$,
∴AB=$\frac{BD}{sin∠BAD}=\frac{2}{sin28°}≈4.260$,
∴⊙O的半径为$\frac{AB}{2}=2.13$.
点评 此题考查切线的性质,关键是根据切线的性质和直径的性质转化为角的关系进行分析.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
9.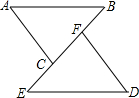 如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
 如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
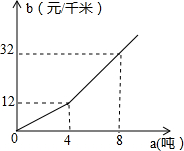 某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.
某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.
 如图,函数y1=ax+b与函数y2=cx+d相交于点A,点A的横坐标为1,若t=y1-y2,则令t>0的x的取值范围是x>1.
如图,函数y1=ax+b与函数y2=cx+d相交于点A,点A的横坐标为1,若t=y1-y2,则令t>0的x的取值范围是x>1.