题目内容
13.已知实数a,b满足:a2+1=$\frac{1}{a}$,b2+1=$\frac{1}{b}$,则2017|a-b|=1.分析 由于a2+1=$\frac{1}{a}$,b2+1=$\frac{1}{b}$,两式相减可得a2-b2=$\frac{1}{a}$-$\frac{1}{b}$,则有(a+b)(a-b)=$\frac{b-a}{ab}$,分解因式可得a=b,依此可得2017|a-b|=20170,再根据零指数幂的计算法则计算即可求解.
解答 解:∵a2+1=$\frac{1}{a}$,b2+1=$\frac{1}{b}$,
(a+b)(a-b)=$\frac{b-a}{ab}$,
[ab(a+b)+1](a-b)=0,
∴a-b=0,即a=b,
∴2017|a-b|=20170=1.
故答案为:1.
点评 此题考查了根与系数的关系,因式分解的应用,零指数幂,本题关键是得到a=b.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据应( )
| A. | 把圆n等分,顺次连接各分点得到的多边形是圆的内接正n边形 | |
| B. | 把圆n等分,依次过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形 | |
| C. | 各边相等.并且各角也相等的多边形是正多边形 | |
| D. | 用量角器等分圆是一种简单而常用的方法 |
 已知:$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{y}_{1}=2}\end{array}\right.$和$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=-1}\end{array}\right.$是一次函数y=kx+b的两组对应值.
已知:$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{y}_{1}=2}\end{array}\right.$和$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=-1}\end{array}\right.$是一次函数y=kx+b的两组对应值.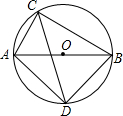 如图,AB为⊙O的直径,AC为⊙O的弦,AB=6,AC=2,∠ACB的平分线交⊙O于点D.
如图,AB为⊙O的直径,AC为⊙O的弦,AB=6,AC=2,∠ACB的平分线交⊙O于点D.