题目内容
当k>0时,双曲线y=
与直线y=-kx的公共点有( )
| k |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
分析:此题可以由k>0判断函数y=
与y=-kx所处的象限,由交点判断函数的公共点个数.
| k |
| x |
解答:解:根据函数y=-kx与y=
(k≠0)的图象特点:
∵k>0时,-k<0,
∴y=-kx的图象过二、四象限,y=
(k≠0)的图象在一、三象限,
∴两图象无交点.
故选A.
| k |
| x |
∵k>0时,-k<0,
∴y=-kx的图象过二、四象限,y=
| k |
| x |
∴两图象无交点.
故选A.
点评:本题考查了反比例函数与一次函数的交点问题,正确掌握其性质才能灵活解题.

练习册系列答案
相关题目
当k<0时,双曲线y=
与直线y=-kx( )
| k |
| x |
| A、没有交点 |
| B、只有一个交点 |
| C、有两个交点 |
| D、有三个交点 |
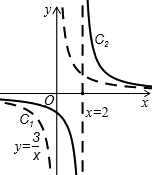 线部分),对于新的双曲线C2,下列结论:
线部分),对于新的双曲线C2,下列结论: 如图,一次函数y=ax+b的图象与反比例函数
如图,一次函数y=ax+b的图象与反比例函数