题目内容
当k>0时,双曲线y=| k | x |
分析:将两个解析式组成方程组,判断出方程组解的个数,即为双曲线y=
与直线y=-kx的交点的个数.
| k |
| x |
解答:解:将y=
与y=-x组成方程组得:
,
①代入②得,
=-x,
∵k>0,
∴x2=-1<0,
故方程组无解,两函数交点个数为0.
| k |
| x |
|
①代入②得,
| k |
| x |
∵k>0,
∴x2=-1<0,
故方程组无解,两函数交点个数为0.
点评:解答此题要将解析式组成方程组,判断出方程组解的个数,进而判断出交点的坐标的个数,体现了数形结合的思想.

练习册系列答案
相关题目
当k>0时,双曲线y=
与直线y=-kx的公共点有( )
| k |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
当k<0时,双曲线y=
与直线y=-kx( )
| k |
| x |
| A、没有交点 |
| B、只有一个交点 |
| C、有两个交点 |
| D、有三个交点 |
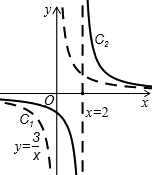 线部分),对于新的双曲线C2,下列结论:
线部分),对于新的双曲线C2,下列结论: 如图,一次函数y=ax+b的图象与反比例函数
如图,一次函数y=ax+b的图象与反比例函数