题目内容
12. 等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P.
等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P.(1)运动几秒后,△ADE为直角三角形?
(2)在点D、E运动时,线段PD与线段PE相等吗?如果相等,给以证明;如不相等,说明理由.
分析 (1)根据等边三角形的性质和直角三角形的性质求出∠AED=30°,根据直角三角形的性质列出关系式,计算即可;
(2)过D点作DH∥AF交BC于点H,证明△DGP≌△EBP,根据全等三角形的性质定理证明即可.
解答 解:(1)∵△ABC是等边三角形,
∴∠A=60°,
△ADE为直角三角形时,∠ADE=90°,
则∠AED=30°,
∴AD=$\frac{1}{2}$AE,即4-0.5t=$\frac{1}{2}$(4+0.5t),
t=$\frac{8}{3}$,
答:运动$\frac{8}{3}$秒后,△ADE为直角三角形;
(2)PD=PE.
证明:过D点作DH∥AF交BC于点H,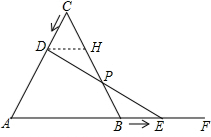
则△CDH为等边三角形,∠HDP=∠PEB,
∴DH=DC,又DC=BE,
∴DH=BE,
在△DGP和△EBP中,
$\left\{\begin{array}{l}{∠HDP=∠BEP}\\{∠DPH=∠EPB}\\{DH=BE}\end{array}\right.$,
∴△DGP≌△EBP,
∴PD=PE.
点评 本题考查的是全等三角形的判定和性质、等边三角形的性质,掌握三角形全等是判判定定理、平行线的性质、等边三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
7.一个物体作左右方向的运动,规定向右运动5m记作+5m,那么向左运动5m记作( )
| A. | -5m | B. | 5m | C. | 10m | D. | -10m |
7.在-2,0.07,0,$\frac{1}{3}$这四个数中,既不是正数也不是负数的是( )
| A. | -2 | B. | 0.07 | C. | 0 | D. | $\frac{1}{3}$ |
 如图,在等边△ABC中,AC=4,点D、E、F分别在三边AB、BC、AC上,且AF=1,FD⊥DE,∠DFE=60°,则AD的长为( )
如图,在等边△ABC中,AC=4,点D、E、F分别在三边AB、BC、AC上,且AF=1,FD⊥DE,∠DFE=60°,则AD的长为( ) 已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P. 如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D. 在下面给出的数轴中,点A表示1,点B表示-2,回答下面的问题:
在下面给出的数轴中,点A表示1,点B表示-2,回答下面的问题: 操作探究:已知在纸面上有一数轴(如图所示),
操作探究:已知在纸面上有一数轴(如图所示), 某地因持续高温干旱,村民饮水困难,镇政府组织村民组成水源行动小组到村镇周边找水.某村民在山洞C里发现了暗河(如图所示),经勘察,在山洞的西面有一条南北走向的公路连接着A,B两村庄,山洞C位于A村庄南偏东30°方向,且位于B村庄南偏东60°方向.为方便A,B两村庄的村民取水,准备从山洞C处向公路AB紧急修建一条最近的简易公路CD,现已知A,B两村庄相距6千米.
某地因持续高温干旱,村民饮水困难,镇政府组织村民组成水源行动小组到村镇周边找水.某村民在山洞C里发现了暗河(如图所示),经勘察,在山洞的西面有一条南北走向的公路连接着A,B两村庄,山洞C位于A村庄南偏东30°方向,且位于B村庄南偏东60°方向.为方便A,B两村庄的村民取水,准备从山洞C处向公路AB紧急修建一条最近的简易公路CD,现已知A,B两村庄相距6千米.