题目内容
11.某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
分析 (1)根据两种产品所需要的甲、乙两种原料列出不等式组,然后求解即可;
(2)根据总利润等于两种产品的利润之和列式整理,然后根据一次函数的增减性求出最大利润即可.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{5x+3(30-x)≤130}\\{4x+6(30-x)≤144}\end{array}\right.$,
解得18≤x≤20,
∵x是正整数,
∴x=18、19、20,
共有三种方案:
方案一:A产品18件,B产品12件,
方案二:A产品19件,B产品11件,
方案三:A产品20件,B产品10件;
(2)根据题意得:y=:700x+900(30-x)=-200x+27000,
∵-200<0,
∴y随x的增大而减小,
∴x=18时,y有最大值,
y最大=-200×18+27000=23400元.
答:利润最大的方案是方案一:A产品18件,B产品12件,最大利润为23400元.
点评 本题考查了一次函数的应用,一元一次不等式组的应用,读懂题目信息,准确找出题中的等量关系和不等量关系是解题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
2.株洲市展览馆某天四个时间段进出馆人数统计如下,则馆内人数变化最大时间段为( )
| 9:00-10:00 | 10:00-11:00 | 14:00-15:00 | 15:00-16:00 | |
| 进馆人数 | 50 | 24 | 55 | 32 |
| 出馆人数 | 30 | 65 | 28 | 45 |
| A. | 9:00-10:00 | B. | 10:00-11:00 | C. | 14:00-15:00 | D. | 15:00-16:00 |
16.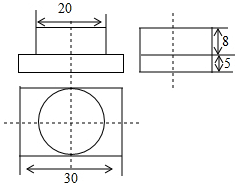 如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
 如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )| A. | 800π+1200 | B. | 160π+1700 | C. | 3200π+1200 | D. | 800π+3000 |
20. 如图,由四个正方体组成的几何体的左视图是( )
如图,由四个正方体组成的几何体的左视图是( )
 如图,由四个正方体组成的几何体的左视图是( )
如图,由四个正方体组成的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
 为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为${y}_{1}=\left\{\begin{array}{l}{{k}_{1}x(0≤x<600)}\\{{k}_{2}x+b(600≤x≤1000)}\end{array}\right.$,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.01x2-20x+30000(0≤x≤1000).
为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为${y}_{1}=\left\{\begin{array}{l}{{k}_{1}x(0≤x<600)}\\{{k}_{2}x+b(600≤x≤1000)}\end{array}\right.$,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.01x2-20x+30000(0≤x≤1000).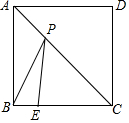 如图所示,正方形ABCD的边长为4,E是边BC上的一点,且BE=1,P是对角线AC上的一动点,连接PB、PE,当点P在AC上运动时,△PBE周长的最小值是6.
如图所示,正方形ABCD的边长为4,E是边BC上的一点,且BE=1,P是对角线AC上的一动点,连接PB、PE,当点P在AC上运动时,△PBE周长的最小值是6.