题目内容
15.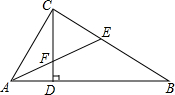 如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求:
如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求:(1)CD的长;
(2)△ABC的角平分线AE交CD于点F,交BC于E点,求证:∠CFE=∠CEF.
分析 (1)根据三角形的面积公式列式计算即可;
(2)根据直角三角形的性质和角平分线的定义证明即可.
解答 解:(1)由题意得,$\frac{1}{2}$×AB×CD=$\frac{1}{2}$×AC×BC,
即$\frac{1}{2}×$CD×10=$\frac{1}{2}×$6×8,
解得CD=$\frac{24}{5}$;
(2)∵∠ACB=90°,
∴∠CAE+∠CEF=90°,
∵CD是AB边上的高,
∴∠FAD+∠AFD=90°,
∵AE是∠CAB的平分线,
∴∠CAE=∠FAD,
∴∠CEF=∠AFD,又∵∠AFD=∠CFE,
∴∠CFE=∠CEF.
点评 本题考查的是勾股定理的应用、直角三角形的性质,掌握直角三角形的面积公式、直角三角形的两锐角互余是解题的关键.

练习册系列答案
相关题目
10.小强买了张50元的乘车IC卡,如果他乘车的次数用m表示,则记录他每次乘车后的余额n(元)如下表:
(1)写出乘车的次数m表示余额n的关系式.
(2)利用上述关系式计算小强乘了10次车还剩下多少元?
(3)小强最多能乘几次车?
| 次数 m | 余额 n(元) |
| 1 | 50-0.9 |
| 2 | 50-1.8 |
| 3 | 50-2.7 |
| 4 | 50-3.6 |
| … | … |
(2)利用上述关系式计算小强乘了10次车还剩下多少元?
(3)小强最多能乘几次车?
7.把下列图形:①线段,②直角三角形,③锐角,④平行四边形,⑤长方形,沿着某条直线对折,这条直线两旁的部分能够完全重合的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.一个多边形截去一个角后,形成的新多边形的内角和其其外角和的2倍,那么原多边形的边数为( )
| A. | 5 | B. | 5或6 | C. | 4或5或6 | D. | 5或6或7 |
 如图,在四边形ABCD中,对角线AC,BD交于点O,AC与BD互相垂直且平分,BD=6,AC=8,则四边形周长为20,面积为24.
如图,在四边形ABCD中,对角线AC,BD交于点O,AC与BD互相垂直且平分,BD=6,AC=8,则四边形周长为20,面积为24.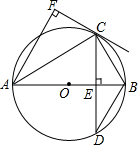 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,垂足为点F,且CF=CE,连接AC,
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,垂足为点F,且CF=CE,连接AC,