题目内容
6. 如图,在四边形ABCD中,对角线AC,BD交于点O,AC与BD互相垂直且平分,BD=6,AC=8,则四边形周长为20,面积为24.
如图,在四边形ABCD中,对角线AC,BD交于点O,AC与BD互相垂直且平分,BD=6,AC=8,则四边形周长为20,面积为24.
分析 首先由AC与BD互相垂直且平分,可证得四边形ABCD是菱形,又由BD=6,AC=8,即可求得答案.
解答 解:∵AC与BD互相垂直且平分,
∴AD=AB=BC=CD,
∴四边形ABCD是菱形,
∵BD=6,AC=8,
∴OA=$\frac{1}{2}$AC=4,OB=$\frac{1}{2}$BD=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
∴四边形周长为:20,面积为:$\frac{1}{2}$×6×8=24.
故答案为:20,24.
点评 此题考查了菱形的判定与性质以及线段垂直平分线的性质.注意证得四边形ABCD是菱形是解此题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
11.当圆的半径发生变化时,面积也发生变化,圆面积S与半径r的关系为S=πr2.下面的说法中,正确的是( )
| A. | S,π,r都是变量 | B. | 只有r是变量 | ||
| C. | S,r是变量,π是常量 | D. | S,π,r都是常量 |
18.下列说法正确的是( )
| A. | a的倒数是$\frac{1}{a}$ | B. | 任何有理数都有倒数 | ||
| C. | -$\frac{1}{4}$的倒数是-4 | D. | $\frac{1}{2}$的倒数是-2 |
16.下列命题中,逆命题为真命题的是( )
| A. | 四边形是多边形 | B. | 两直线平行,同旁内角互补 | ||
| C. | 如果a=0,b=0,那么ab=0 | D. | 相等的两个数平方一定相等 |
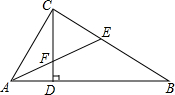 如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求:
如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求: