题目内容
1. 如图,在△ABC中,∠C=90°,内切圆⊙O与AB相切于点E,BO的延长线交AC于点D,求证:BE•BD=BO•BC.
如图,在△ABC中,∠C=90°,内切圆⊙O与AB相切于点E,BO的延长线交AC于点D,求证:BE•BD=BO•BC.
分析 连结OE,如图,根据切线的性质得OE⊥AB,根据三角形内心的性质得OB平分∠ABC,则∠OEB=90°,∠OBE=∠OBC,由于∠OBE=∠DBC,∠OEB=∠C,则可判断△OBE∽△DBC,然后利用相似的性质得BE:BC=BO:BD,然后化为等积式即可得到结论.
解答  证明:连结OE,如图,
证明:连结OE,如图,
∵⊙O为△ABC的内切圆,
∴OE⊥AB,OB平分∠ABC,
∴∠OEB=90°,∠OBE=∠OBC,
∴∠OBE=∠DBC,∠OEB=∠C,
∴△OBE∽△DBC,
∴BE:BC=BO:BD,
∴BE•BD=BO•BC.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆;三角形的内心就是三角形三个内角角平分线的交点.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
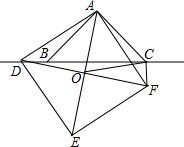 已知,如图,在Rt△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一
已知,如图,在Rt△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一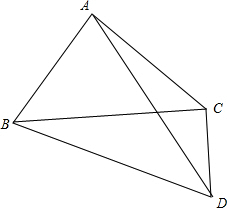 如图,在△ABC中,AB=AC,点D为△ABC外一点,连接AD,BD,CD,∠BAD=3∠CAD,∠ADC=30°,求证:∠DBC=30°.
如图,在△ABC中,AB=AC,点D为△ABC外一点,连接AD,BD,CD,∠BAD=3∠CAD,∠ADC=30°,求证:∠DBC=30°. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).