题目内容
5.用配方法解方程:(1)2x2+2.5x-0.125=0;
(2)4x2+5x+1=0;
(3)2x2+5x-3=0.
分析 (1)先把小数系数化为分数,再把二次项系数化为1得到x2+$\frac{5}{4}$x=$\frac{1}{16}$,接着利用配方法得(x+$\frac{5}{8}$)2=$\frac{29}{64}$,然后利用直接开平方法解方程;
(2)先把二次项系数化为1得到x2+$\frac{5}{4}$x=-$\frac{1}{4}$,再利用配方法得(x+$\frac{5}{8}$)2=$\frac{9}{64}$,然后利用直接开平方法解方程;
(3)先把二次项系数化为1得到x2+$\frac{5}{2}$x=$\frac{3}{2}$,再利用配方法得(x+$\frac{5}{4}$)2=$\frac{49}{16}$,然后利用直接开平方法解方程.
解答 解:(1)x2+$\frac{5}{4}$x=$\frac{1}{16}$,
x2+$\frac{5}{4}$x+($\frac{5}{8}$)2=$\frac{1}{16}$+($\frac{5}{8}$)2,
(x+$\frac{5}{8}$)2=$\frac{29}{64}$,
x+$\frac{5}{8}$=±$\frac{\sqrt{29}}{8}$,
所以x1=$\frac{-5+\sqrt{29}}{8}$,x2=$\frac{-5-\sqrt{29}}{8}$;
(2)x2+$\frac{5}{4}$x=-$\frac{1}{4}$,
x2+$\frac{5}{4}$x+($\frac{5}{8}$)2=-$\frac{1}{4}$+($\frac{5}{8}$)2,
(x+$\frac{5}{8}$)2=$\frac{9}{64}$,
x+$\frac{5}{8}$=±$\frac{3}{8}$,
所以x1=-1,x2=-$\frac{1}{4}$;
(3)x2+$\frac{5}{2}$x=$\frac{3}{2}$,
x2+$\frac{5}{2}$x+($\frac{5}{4}$)2=$\frac{3}{2}$+($\frac{5}{4}$)2,
(x+$\frac{5}{4}$)2=$\frac{49}{16}$,
x+$\frac{5}{4}$=±$\frac{7}{4}$,
所以x1=-3,x2=$\frac{1}{2}$.
点评 本题考查了配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案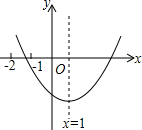 已知二次函数y=ax2+bx+c(a≠0)≠的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a-b=0;④8a+c<0;⑤9a+3b+c<0.其中结论正确的个数有( )
已知二次函数y=ax2+bx+c(a≠0)≠的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a-b=0;④8a+c<0;⑤9a+3b+c<0.其中结论正确的个数有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 1,2,3 | B. | 2,2,4 | C. | 1,2,4 | D. | 3,4,5 |
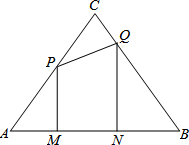 如图,等边三角形ABC的边长为8cm,动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、QN,垂足分别为点M、N.设P、Q两点运动时间为t秒(0<t<4),四边形MNQP的面积为Scm2.
如图,等边三角形ABC的边长为8cm,动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、QN,垂足分别为点M、N.设P、Q两点运动时间为t秒(0<t<4),四边形MNQP的面积为Scm2.