Question

11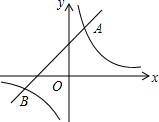．如图，已知在平面直角坐标系中，O是坐标原点，点A（2，5）在反比例函数y=$\frac{k}{x}$的图象上．一次函数y=x+b的图象过点A，且与反比例函数图象的另一交点为B．
（1）求k和b的值；
（2）设反比例函数值为y₁，一次函数值为y₂，求y₁＞y₂时x的取值范围．

Answer 1

分析 （1）把A（2，5）分别代入$y=\frac{k}{x}$和y=x+b，即可求出k和b的值；
（2）联立一次函数和反比例函数的解析式，求出交点坐标，进而结合图形求出y₁＞y₂时x的取值范围．

解答 解：（1）把A（2，5）分别代入$y=\frac{k}{x}$和y=x+b，
得$\left\{\begin{array}{l}\frac{k}{2}=5\\ 2+b=5\end{array}\right.$，
解得k=10，b=3；   
（2）由（1）得，直线AB的解析式为y=x+3，
反比例函数的解析式为$y=\frac{10}{x}$．                   
由$\left\{\begin{array}{l}y=\frac{10}{x}\\ y=x+3\end{array}\right.$，解得：$\left\{\begin{array}{l}x=2\\ y=5\end{array}\right.$或$\left\{\begin{array}{l}x=-5\\ y=-2\end{array}\right.$．      
则点B的坐标为（-5，-2）．
由图象可知，当y₁＞y₂时，x的取值范围是x＜-5或0＜x＜2．

点评 本题主要考查了反比例函数与一次函数的交点问题，解题的关键是求出k和b的值，此题难度不大．