题目内容
12.小亮玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子的颗数与所得分数的对应关系如表所示:| 挪动珠子数(颗) | 2 | 3 | 4 | 5 | 6 | … |
| 所得分数 | 5 | 11 | 19 | 29 | 41 | … |
分析 观察表格可找出挪动n颗珠子时(n为大于1的整数)得分为n2+(n-1),根据所得分数为155分即可得出关于n的一元二次方程,解之即可得出结论.
解答 解:观察表格,可发现:5=22+1,11=32+2,19=42+3,29=52+4,41=62+5,…,
∴挪动n颗珠子时(n为大于1的整数)得分为n2+(n-1).
根据题意得:n2+n-1=155,
解得:n=12或n=-13(舍去).
故答案为:12
点评 本题考查了一元二次方程的应用以及规律型中数字的变化,根据表格寻找到挪动n颗珠子时(n为大于1的整数)得分为n2+(n-1)是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
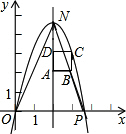 如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).
如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).
 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为2.
如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为2.