题目内容
19. 如图,在等边△ABC中,点D、E分别在边BC、AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.求证:PQ=$\frac{1}{2}$BP.
如图,在等边△ABC中,点D、E分别在边BC、AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.求证:PQ=$\frac{1}{2}$BP.
分析 根据全等三角形的判定方法SAS可证得△BEC≌△ADB,根据各角的关系及三角形内角、外角和定理可证得∠BPQ=60°,即可得结论.
解答 证明:∵△ABC为等边三角形.
∴AB=AC,∠BAC=∠ACB=60°,
在△BAE和△ACD中,$\left\{\begin{array}{l}{AE=CD}&{\;}\\{∠BAC=∠ACB}&{\;}\\{AB=AC}&{\;}\end{array}\right.$,
∴△BAE≌△ACD(SAS),
∴∠ABE=∠CAD.
∵∠BPQ为△ABP外角,
∴∠BPQ=∠ABE+∠BAD.
∴∠BPQ=∠CAD+∠BAD=∠BAC=60°
∵BQ⊥AD,
∴∠PBQ=30°,
∴PQ=$\frac{1}{2}$BP.
点评 本题主要考查了全等三角形的判定和性质,涉及到等边三角形、直角三角形、三角形内角及外角和定理等知识点,证明三角形全等是解决问题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
7.下列运算正确的是( )
| A. | (-2a2)3=-8a8 | B. | 3a2-a2=2a2 | C. | a6÷a3=a9 | D. | a2×a3=a6 |
14.把抛物线y=x2+1向左平移3个单位,再向下平移2个单位,得到的抛物线的顶点为( )
| A. | (3,-1) | B. | (3,1) | C. | (-3,1) | D. | (-3,-1) |
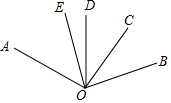 如图,OC,OD,OE是∠AOB内的射线,OD平分∠AOB,OC平分∠BOD,∠DOE=$\frac{1}{3}$∠AOE,若∠COE=45°,求∠AOB的度数.
如图,OC,OD,OE是∠AOB内的射线,OD平分∠AOB,OC平分∠BOD,∠DOE=$\frac{1}{3}$∠AOE,若∠COE=45°,求∠AOB的度数.