题目内容
14.(1)计算:($\frac{1}{3}$)-2+(π-2014)0+sin60°+|$\sqrt{3}$-2|(2)化简求值:$\frac{2}{x+1}$-$\frac{x-2}{{x}^{2}-1}$÷$\frac{{x}^{2}-2x}{{x}^{2}-2x+1}$(其中x=tan60°+1)
分析 (1)首先计算负指数次幂、0次幂、特殊角的三角函数值以及去掉绝对值符号,最后合并同类二次根式即可;
(2)分式的分子、分母分解因式,除法转化为乘法,计算乘法,再进行加减运算即可化简,然后把x的值化简,代入求值.
解答 解:(1)解:原式=9+1+$\frac{\sqrt{3}}{2}$+2-$\sqrt{3}$=12-$\frac{\sqrt{3}}{2}$;
(2)原式=$\frac{2}{x+1}$-$\frac{x-2}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x(x-2)}$
=$\frac{2}{x+1}$-$\frac{x-1}{x(x+1)}$
=$\frac{2x-(x-1)}{x(x+1)}$
=$\frac{x+1}{x(x+1)}$
=$\frac{1}{x}$.
当x=tan60°+1=$\sqrt{3}$+1时,原式=$\frac{1}{\sqrt{3}+1}$=$\frac{\sqrt{3}-1}{2}$.
点评 本题考查实数的运算以及分式的化简求值,正确对分式进行通分、约分是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.能说明命题“对于任何实数a,a2≥a”是假命题的一个反例可以是( )
| A. | a=-2 | B. | a=1 | C. | a=0 | D. | a=0.2 |
6.下列四组线段中,能组成三角形的是( )
| A. | 2cm,3cm,4cm | B. | 3cm,4cm,7cm | C. | 4cm,6cm,2cm | D. | 7cm,10cm,2cm |
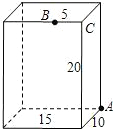 如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
 如图,在平面直角坐标系中,一次函数y=kx+4的图象经过点A(1,3),点B是一次函数y=kx+4的图象与正比例函数y=$\frac{1}{3}$x的图象的交点.
如图,在平面直角坐标系中,一次函数y=kx+4的图象经过点A(1,3),点B是一次函数y=kx+4的图象与正比例函数y=$\frac{1}{3}$x的图象的交点.