题目内容
一元二次方程3x2-8x+m=0的两根之比为3:1,求m的值.
考点:根与系数的关系
专题:计算题
分析:设方程的两根为t,3t,根据根与系数的关系得t+3t=
,t•3t=
,然后先计算出t的值,然后进行m的值.
| 8 |
| 3 |
| m |
| 3 |
解答:解:设方程的两根为t,3t,
根据题意得t+3t=
,t•3t=
,
所以t=
,
所以m=3×
×3×
=4.
根据题意得t+3t=
| 8 |
| 3 |
| m |
| 3 |
所以t=
| 2 |
| 3 |
所以m=3×
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
使式子|2013+m|=|-2013|+|m|成立的m必为( )
| A、正数 | B、负数 |
| C、正数或零 | D、负数或零 |
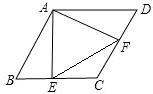 如图,在菱形ABCD中,E、F分别是CB、CD上的点,BE=DF,连接E、F,若E、F分别是CB、CD的中点,△AEF为等边三角形.求证:AE垂直平分BC.
如图,在菱形ABCD中,E、F分别是CB、CD上的点,BE=DF,连接E、F,若E、F分别是CB、CD的中点,△AEF为等边三角形.求证:AE垂直平分BC.