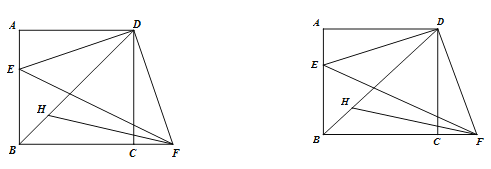Question

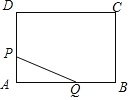
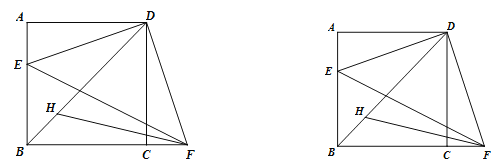
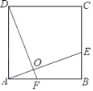
【题目】如图，在正方形ABCD中，AF=BE，AE与DF相交于于点O．

（1）求证：△DAF≌△ABE；

（2）求∠AOD的度数；

（3）若AO=4，DF=10，求的值.

Answer 1

【答案】（1）见解析；（2）；（3）tan∠ADF的值为.

【解析】

(1)利用正方形的性质得出AD=AB,∠DAB=∠ABC=90°,即可得出结论;

(2)利用(1)的结论得出∠ADF=∠BAE,进而求出∠ADF+∠DAO=90°,最后用三角形的内角和定理即可得出结论.

（3）根据（2）得到AO2=OF·OD，再设OF=x,DO=10-x，求出x即可解答

(1)在正方形ABCD中，DA=AB,,

又AF=BE

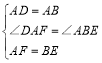
≌ (SAS)

（2）由（1）得 ≌ ，

ADF=BAE,

又 BAE+DAO=,ADF+DAO=

（3）由（2）得∠AOD=900 ∴△AOF∽△DOA ∴AO2=OF·OD

设OF=x,DO=10-x ∴x(10-x)=16 解得x=2或x=8（舍去）

∴tan∠ADF=

∴tan∠ADF的值为.