题目内容
14．在Rt△ABC中，∠C=90°，AB=4，AC=1，则tanA的值是（ ）| A． | $\frac{{\sqrt{15}}}{4}$ | B． | $\sqrt{15}$ | C． | $\frac{1}{4}$ | D． | 4 |
分析 首先利用勾股定理得出BC的长，再利用锐角三角函数关系得出tanA的值．
解答 
解：如图所示：
∵∠C=90°，AB=4，AC=1，
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{15}$，
则tanA=$\frac{BC}{AC}$=$\frac{\sqrt{15}}{1}$=$\sqrt{15}$．
故选：B．
点评 此题主要考查了锐角三角函数关系，正确记忆边角关系是解题关键．
练习册系列答案
相关题目
4．在平面直角坐标系中，在x轴上的点是（ ）
| A． | （-1，2） | B． | （-2，-3） | C． | （0，3） | D． | （-3，0） |
19．下列分式与分式$\frac{2y}{x}$相等的是（ ）
| A． | $\frac{4{y}^{2}}{{x}^{2}}$ | B． | $\frac{2xy}{{x}^{2}}$ | C． | $\frac{y}{2x}$ | D． | -$\frac{-2y}{-x}$ |
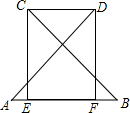如图，已知：∠A=∠B，CE⊥AB，DF⊥AB，垂足分别为E，F，AD=BC．求证：AE=BF．