题目内容
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程组![]() 的解,点C是直线
的解,点C是直线![]() 与直线AB的交点,点D在线段OC上,OD=
与直线AB的交点,点D在线段OC上,OD=![]()
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形(邻边相等的平行四边形)?若存在,请写出点Q的坐标;若不存在,请说明理由.
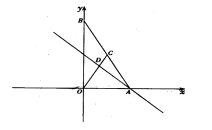
【答案】(1)C点的坐标是(3,6);(2)AD的函数解析式为y=x+6;(3)Q1(3![]() ,3
,3![]() )、Q2(3
)、Q2(3![]() ,3
,3![]() )、Q3(6,6)、Q4(3,3).
)、Q3(6,6)、Q4(3,3).
【解析】
(1)根据解方程组,可得A、B的坐标,根据待定系数法,可得函数解析式,根据解方程组,可得点C的坐标;
(2)根据D在OC上,OD=![]() ,可得方程组,根据解方程组,可得D点坐标,根据待定系数法,可得AD的函数解析式;
,可得方程组,根据解方程组,可得D点坐标,根据待定系数法,可得AD的函数解析式;
(3)结合菱形的性质,分情况讨论:若P在x轴上方,若P在x轴下方,若Q在x轴上方,若Q在x轴下方,进行计算即可得到答案.
(1)解![]() ,得
,得![]() ,即A(6,0)、B(0,12).设直线AB的解析式y=kx+b,把A、B点的坐标代入函数解析式,得
,即A(6,0)、B(0,12).设直线AB的解析式y=kx+b,把A、B点的坐标代入函数解析式,得![]() ,解得
,解得![]() .直线AB的解析式y=2x+12,由点C是直线y=2x与直线AB的交点,得
.直线AB的解析式y=2x+12,由点C是直线y=2x与直线AB的交点,得![]() ,解得
,解得![]() ,C点的坐标是(3,6);
,C点的坐标是(3,6);
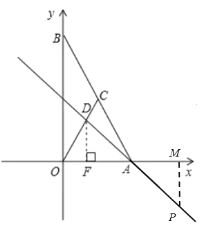
(2)由点D在线段OC上,OD=![]() ,
,
得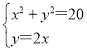 ,解得
,解得![]() ,即D点坐标是(2,4)
,即D点坐标是(2,4)
设AD的函数解析式为y=kx+b,把A、D点的坐标代入,得![]()
,解得![]() .
.
AD的函数解析式为y=x+6;
(3)过D作DF⊥x轴,由(2)中D的坐标可知,则DF=AF=4,所以∠OAD=45°,因为以O、A、P、Q为顶点的四边形是菱形,所以需分情况讨论:
若P在x轴上方,OAPQ是菱形,则PQ∥OA,PQ=OA=/span>6=AP,过P作PM⊥x轴,
如图所示,

因为∠OAD=45°,由三角函数可得PM=AM=![]() =3
=3![]() ,OM=63
,OM=63![]() ,即P(63
,即P(63![]() ,3
,3![]() ),
),
所以Q的横坐标为63![]() 6=3
6=3![]() ,Q1(3
,Q1(3![]() ,3
,3![]() );
);
若P在x轴下方,OAPQ是菱形,则PQ∥OA,PQ=OA=6=AP.过P作PM⊥x轴,
如图所示,
因为∠MAP=∠OAD=45°,由三角函数得到PM=AM=![]() =3
=3![]() ,OM=6+3
,OM=6+3![]() ,即P(6+3
,即P(6+3![]() ,3
,3![]() ),
),
所以Q的横坐标为6+3![]() 6=3
6=3![]() ,Q2(3
,Q2(3![]() ,3
,3![]() );
);
若Q在x轴上方,OAQP是菱形,则∠OAQ=2∠OAD=90°,所以此时OAQP是正方形.
又因正方形边长为6,所以此时Q3(6,6);
若Q在x轴下方,OPAQ是菱形,则∠PAQ=2∠OAD=90°,
所以此时OPAQ是正方形.又因正方形对角线为6,
由正方形的对称性可得Q4(3,/span>3).

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案