题目内容
7.在四边形ABCD中AB=3,AD=DC=4,∠A=120°,BD平分∠ABC.那么四边形ABCD的面积为10$\sqrt{3}$..分析 过D作DE⊥BA于E,DF⊥BC于F,根据角平分线的性质得到DE=DF,根据全等三角形的性质得到BE=BF,AE=CF,解直角三角形得到AE=$\frac{1}{2}$AD=2,DE=2$\sqrt{3}$根据三角形的面积公式即可得到结论.
解答  解:过D作DE⊥BA于E,DF⊥BC于F,
解:过D作DE⊥BA于E,DF⊥BC于F,
∵BD平分∠ABC.
∴DE=DF,
在Rt△BED与Rt△BFD中$\left\{\begin{array}{l}{DE=DF}\\{AD=AD}\end{array}\right.$,
∴Rt△BED≌Rt△BFD,
∴BE=BF,
在Rt△AED与Rt△CFD中$\left\{\begin{array}{l}{DE=DF}\\{AD=CD}\end{array}\right.$,
∴Rt△AED≌Rt△CFD,
∴AE=CF,
∵∠BAD=120°,
∴∠EAD=60°,
∴AE=$\frac{1}{2}$AD=2,DE=2$\sqrt{3}$
∴BC=7,
∴四边形ABCD的面积=S△ABD+D△BCD=$\frac{1}{2}×$3×2$\sqrt{3}$+$\frac{1}{2}×$7×2$\sqrt{3}$=10$\sqrt{3}$,
故答案为:10$\sqrt{3}$.
点评 本题考查了角平分线的性质,全等三角形的判断和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
17.2016年3月5日,李克强总理在第十二届全国人大第四次会议上作政府工作报告,报告中谈到2015年我国GDP达到67.67万亿元,排名世界第二.数据67.67万亿用学记数法可表示为6.767×10n,则n等于( )
| A. | 5 | B. | 9 | C. | 13 | D. | 15 |
18.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
| 投资量x(万元) | 2 |
| 种植树木利润y1(万元) | 4 |
| 种植花卉利润y2(万元) | 2 |
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
12.按照下面的操作步骤,若输入x=-4,则输出的值为( )

| A. | 3 | B. | -3 | C. | -5 | D. | 5 |
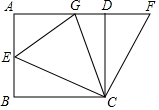 如图1,在边长4的正方形ABCD中,E是AB边上一动点(不与A、B重合),F是AD延长线上一点,且满足DF=BE,以CE为边作∠ECG=45°,交AD于点G.
如图1,在边长4的正方形ABCD中,E是AB边上一动点(不与A、B重合),F是AD延长线上一点,且满足DF=BE,以CE为边作∠ECG=45°,交AD于点G.