题目内容
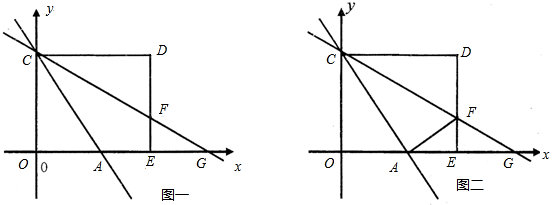
已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.

(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.

(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
考点:圆周角定理,等边三角形的判定与性质,勾股定理
专题:证明题
分析:(Ⅰ)利用圆周角定理可以判定△CAB和△DCB是直角三角形,利用勾股定理可以求得AC的长度;利用圆心角、弧、弦的关系推知△DCB也是等腰三角形,所以利用勾股定理同样得到BD=CD=5
;
(Ⅱ)如图②,连接OB,OD.由圆周角定理、角平分线的性质以及等边三角形的判定推知△OBD是等边三角形,则BD=OB=OD=5.
| 2 |
(Ⅱ)如图②,连接OB,OD.由圆周角定理、角平分线的性质以及等边三角形的判定推知△OBD是等边三角形,则BD=OB=OD=5.
解答: 解:(Ⅰ)如图①,∵BC是⊙O的直径,
解:(Ⅰ)如图①,∵BC是⊙O的直径,
∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6,
∴由勾股定理得到:AC=
=
=8.
∵AD平分∠CAB,
∴
=
,
∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,
∴易求BD=CD=5
;
(Ⅱ)如图②,连接OB,OD.
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB=
∠CAB=30°,
∴∠DOB=2∠DAB=60°.
又∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB=OD.
∵⊙O的直径为10,则OB=5,
∴BD=5.
 解:(Ⅰ)如图①,∵BC是⊙O的直径,
解:(Ⅰ)如图①,∵BC是⊙O的直径,∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6,
∴由勾股定理得到:AC=
| BC2-AB2 |
| 102-62 |
∵AD平分∠CAB,
∴
 |
| CD |
 |
| BD |
∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,
∴易求BD=CD=5
| 2 |
(Ⅱ)如图②,连接OB,OD.
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB=
| 1 |
| 2 |
∴∠DOB=2∠DAB=60°.
又∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB=OD.
∵⊙O的直径为10,则OB=5,
∴BD=5.
点评:本题综合考查了圆周角定理,勾股定理以及等边三角形的判定与性质.此题利用了圆的定义、有一内角为60度的等腰三角形为等边三角形证得△OBD是等边三角形.

练习册系列答案
相关题目
载有239名乘客的马航飞机失联后,其行踪一直成为世人关注的焦点.小明在百度中搜到最新的消息32800000个,其中32800000用科学记数法表示为( )
| A、3.28×105 |
| B、3.28×106 |
| C、3.28×107 |
| D、3.28×108 |
 已知:如图,在△ABC中,AB=AC,D为BC上的一点,DA平分∠EDC,且∠E=∠B.求证:△ADE≌△ADC.
已知:如图,在△ABC中,AB=AC,D为BC上的一点,DA平分∠EDC,且∠E=∠B.求证:△ADE≌△ADC. 如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,求∠2的度数.
如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,求∠2的度数.