题目内容
某批篮球质量检验结果如下:
(1)填写表中优等品的频率;
(2)这批篮球优等品的概率估计值是多少?
| 抽取的篮球数n | 400 | 600 | 800 | 1000 | 1200 |
| 优等品频数m | 376 | 570 | 744 | 940 | 1128 |
| 优等品频率m/n | 0.94 |
(2)这批篮球优等品的概率估计值是多少?
考点:利用频率估计概率
专题:
分析:先求出频率,再根据频率估计出概率.
解答:解:(1)如下表:
(2)这批篮球优等品的概率估计值是0.94.
| 抽取的篮球数n | 400 | 600 | 800 | 1000 | 1200 |
| 优等品频数m | 376 | 570 | 744 | 940 | 1128 |
| 优等品频率m/n | 0.94 | 0.95 | 0.93 | 0.94 | 0.94 |
点评:考查利用频率估计概率,其根据是概率的频率定义.
在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示一定的稳定性.这个固定数定义为该事件的概率,这就是概率的频率定义.用到的知识点为:频率=所求情况数与总情况数之比.
在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示一定的稳定性.这个固定数定义为该事件的概率,这就是概率的频率定义.用到的知识点为:频率=所求情况数与总情况数之比.

练习册系列答案
相关题目
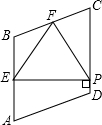 如图,在菱形ABCD中,∠A=80°,E、F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
如图,在菱形ABCD中,∠A=80°,E、F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )| A、40° | B、45° |
| C、50° | D、55° |
下列命题是真命题的共有( )
(1)对顶角相等;
(2)邻补角相等;
(3)同位角相等;
(4)在同一平面内,不平行的两条直线一定垂直;
(5)两直平行线被被第三条直线所截,一对内错角的角平分线互相平行.
(1)对顶角相等;
(2)邻补角相等;
(3)同位角相等;
(4)在同一平面内,不平行的两条直线一定垂直;
(5)两直平行线被被第三条直线所截,一对内错角的角平分线互相平行.
| A、1个 | B、2个 | C、3个 | D、4个 |
下列运算正确的是( )
| A、a2+a2=2a4 |
| B、(a2)3=a5 |
| C、a3a3=a9 |
| D、a6÷a3=a3 |
下列选项中,正确是( )
| A、1是最小的自然数 |
| B、正数、零、负数统称为有理数 |
| C、-32的底数为-3 |
| D、a、b互为相反数,则a+b=0 |
 如图,已知BC∥GE,AF∥DE,∠1=50°.
如图,已知BC∥GE,AF∥DE,∠1=50°.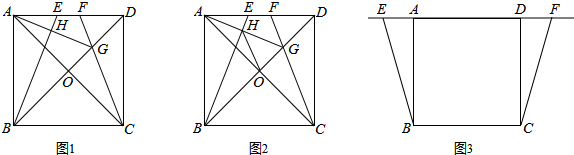
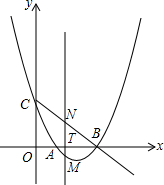 已知:如图,抛物线
已知:如图,抛物线