Question

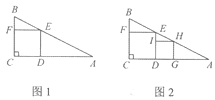
【题目】如图，已知在△ABC中，AB＝AC，点D为BC上一点(不与点B、点C重合)，连结AD，以AD为边在右侧作△ADE，DE交AC于点F，其中AD＝AE，∠ADE＝∠B.

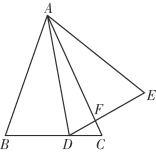
(1)求证：△ABD∽△AEF；

(2)若＝，记△ABD的面积为S1，△AEF的面积为S2，求的值．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）根据等腰三角形的性质得到∠B=∠C，∠ADE=∠E，求得∠B=∠E，于是得到结论；
（2）根据相似三角形的性质即可得到结论．

考查了相似三角形的判定和性质，等腰三角形的性质，熟练掌握相似三角形的性质是解题的关键．

解：(1)证明：∵AB＝AC，

∴∠B＝∠C，

∵AD＝AE，

∴∠ADE＝∠E，

又∵∠ADE＝∠B，

∴∠B＝∠E，

∵∠BDE＝∠ADB＋∠ADE＝∠C＋∠DFC＝∠E＋∠AFE，

∴∠ADB＝∠AFE，

∴△ABD∽△AEF；

(2)由(1)得△ABD∽△AEF，

而＝，

∴