题目内容
抛物线y=﹣x2+15有最__________点,其坐标是__________.
0,15).
【考点】二次函数的最值.
【专题】函数思想.
【分析】根据抛物线的开口方向判断该抛物线的最值情况;根据顶点坐标公式求得顶点坐标.
【解答】解:∵抛物线y=﹣x2+15的二次项系数a=﹣1<0,
∴抛物线y=﹣x2+15的图象的开口方向是向下,
∴该抛物线有最大值;
当x=0时,y取最大值,即y最大值=15;
∴顶点坐标是(0,15).
故答案是:高、(0,15).
【点评】本题考查了二次函数的最值.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
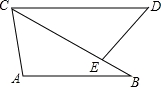

 3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.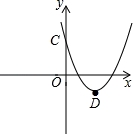
 b=b2﹣a﹣1,例如:7
b=b2﹣a﹣1,例如:7 AOB=35º,
AOB=35º,