题目内容
1.某一公路的道路维修工程,准备从甲、乙两个工程队选一个队单独完成.根据两队每天的工程费用和每天完成的工程量可知,若由两队合做此项维修工程,6天可以完成,共需工程费用385200元,若单独完成此项维修工程,甲队比乙队少用5天,每天的工程费用甲队比乙队多4000元,从节省资金的角度考虑,应该选择哪个工程队?分析 设甲队单独完成此项工程需要x天,乙队单独完成需要(x+5)天,然后依据6天可以完成,列出关于x的方程,从而可求得甲、乙两队单独完成需要的天数,然后设甲队每天的工程费为y元,则可表示出乙队每天的工程费,接下来,根据两队合作6天的工程费用为385200元列方程求解,于是可得到两队独做一天各自的工程费,然后可求得完成此项工程的工程费,从而可得出问题的答案.
解答 解:设甲队单独完成此项工程需要x天,乙队单独完成需要(x+5)天.
依据题意可列方程:$\frac{1}{x}$+$\frac{1}{x+5}$=$\frac{1}{6}$,
解得:x1=10,x2=-3(舍去).
经检验:x=10是原方程的解.
设甲队每天的工程费为y元.
依据题意可列方程:6y+6(y-4000)=385200,
解得:y=34100.
甲队完成此项工程费用为34100×10=341000元.
乙队完成此项工程费用为30100×15=451500元.
答:从节省资金的角度考虑,应该选择甲工程队.
点评 本题主要考查的是分式方程的应用、一元一次方程的应用,根据题意列出关于x的方程是解题的关键.

练习册系列答案
相关题目
12.下列各数中最小的是( )
| A. | -5 | B. | -π | C. | 3 | D. | 0 |
16.下列说法正确的是( )
| A. | “任意画一个三角形,其内角和为360°”是随机事件 | |
| B. | 已知某篮球运动员投篮投中的概率为0.6,则他投十次可投中6次 | |
| C. | 抽样调查选取样本时,所选样本可按自己的喜好选取 | |
| D. | 检测某城市的空气质量,采用抽样调查法 |
6.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a5÷a2=a3 | C. | (-3a)3=-9a3 | D. | 2x2+3x2=5x4 |
13.在函数y=$\frac{\sqrt{x+4}}{x}$中,自变量x的取值范围是( )
| A. | x>0 | B. | x≥-4 | C. | x≥-4且x≠0 | D. | x>0且x≠-1 |
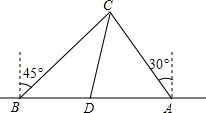 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60($\sqrt{6}+\sqrt{2}$)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120($\sqrt{6}-\sqrt{2}$)海里.
为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60($\sqrt{6}+\sqrt{2}$)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120($\sqrt{6}-\sqrt{2}$)海里.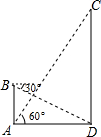 如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.
如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.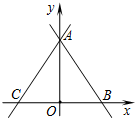 如图,直线AB的函数关系式为y=-$\frac{3}{2}$x+3,直线AC与直线AB关于y轴成轴对称,则直线AC的函数关系式为y=$\frac{3}{2}$x+3.
如图,直线AB的函数关系式为y=-$\frac{3}{2}$x+3,直线AC与直线AB关于y轴成轴对称,则直线AC的函数关系式为y=$\frac{3}{2}$x+3.