题目内容
设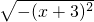 是一个实数,则x=________,若
是一个实数,则x=________,若 和
和 都是实数,则x=________.
都是实数,则x=________.
-3 1
分析:因为负数没有平方根,所以要使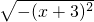 成立,则被开方数必须是0,即x=-3;第二题也是根据二次根式的被开方数是非负数解决问题.
成立,则被开方数必须是0,即x=-3;第二题也是根据二次根式的被开方数是非负数解决问题.
解答:(1)∵-(x+3)2≥0,
∴-(x+3)2=0,
∴x+3=0即x=-3;
(2)∵x-1≥0,1-x≥0
即x≥1,x≤1,
∴x=1.
点评:本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.本题的关键是负数没有平方根这一要点.
分析:因为负数没有平方根,所以要使
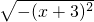 成立,则被开方数必须是0,即x=-3;第二题也是根据二次根式的被开方数是非负数解决问题.
成立,则被开方数必须是0,即x=-3;第二题也是根据二次根式的被开方数是非负数解决问题.解答:(1)∵-(x+3)2≥0,
∴-(x+3)2=0,
∴x+3=0即x=-3;
(2)∵x-1≥0,1-x≥0
即x≥1,x≤1,
∴x=1.
点评:本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.本题的关键是负数没有平方根这一要点.

练习册系列答案
相关题目