题目内容
16.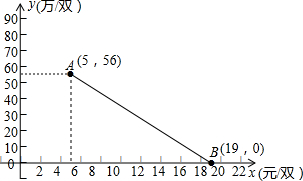 某袜业公司向上海世博会申请了在自己生产的袜子上印上海世博会会徽的专利权,但组委会只允许这种袜子在5月1日至5月31日这一个月内在全国各地生产销售.生产这种袜子的成本为每双5元,该袜业公司经过一段时间调查与分所后,发现这种袜子在5月份销售期间,每双袜子的销售单价x(元)和日均销售量y(万双)满足如图所示关系;日均各种费用等固定成本为20万元.
某袜业公司向上海世博会申请了在自己生产的袜子上印上海世博会会徽的专利权,但组委会只允许这种袜子在5月1日至5月31日这一个月内在全国各地生产销售.生产这种袜子的成本为每双5元,该袜业公司经过一段时间调查与分所后,发现这种袜子在5月份销售期间,每双袜子的销售单价x(元)和日均销售量y(万双)满足如图所示关系;日均各种费用等固定成本为20万元.(1)直接写出y关于x的函数解析式y=-4x+76;
(2)求日均毛利润W万元关于x的函数解析式;(毛利润=钠售利润-固定成本)
(3)若该袜业公司在申请专利和投入生产设备上的总投资为4000万元,请问:在5月份的生产销售后,该公司若想获得最大总利润,这种袜子每双应定价多少元?并求出最大总利润.
分析 (1)根据图象提供的信息列方程组即可得到结论;
(2)根据毛利润=钠售利润-固定成本即可得到日均毛利润W万元关于x的函数解析式;
(3)根据总利润=毛利润-总投资得到函数关系式,求出函数的最大值即可.
解答 解:(1)设y=kx+b,
∴$\left\{\begin{array}{l}{56=5k+b}\\{0=19k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-4}\\{b=76}\end{array}\right.$.
∴y关于x的函数解析式为:y=-4x+76,
故答案为:y=-4x+76;
(2)根据题意得:W=(-4x+76)(x-5)-20,
即:W=-4x2+96x-400,
(3)设总利润为S,
则:S=30×(-4x2+96x-400)-4000=-120(x-12)2+32000,
当x=12时,S最大=32000,
故这种袜子每双应定价12元,最大总利润是32000元.
点评 本题考查了二次函数的应用,一次函数的应用以及用待定系数法求一次函数的综合应用,主要结合一次函数的性质,求出二次函数的最值问题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
4.菱形有一个内角为120°,较短对角线为6,则菱形的周长为( )
| A. | 12 | B. | 24 | C. | 36 | D. | 12$\sqrt{3}$ |
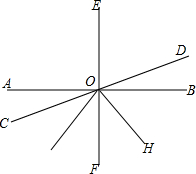 如图,AB、CD、EF相交于点O,EF⊥AB,OG平分∠COF,OH平分∠DOG,若∠AOC:∠DOH=8:29,求∠COH的大小.
如图,AB、CD、EF相交于点O,EF⊥AB,OG平分∠COF,OH平分∠DOG,若∠AOC:∠DOH=8:29,求∠COH的大小.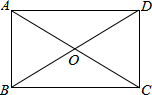 如图,矩形ABCD的两条对角线相交于点O,已知,AB=OA=3cm,求BD与AD的长.
如图,矩形ABCD的两条对角线相交于点O,已知,AB=OA=3cm,求BD与AD的长. 小明在楼顶上看到对面山上有一座铁塔.他现有的测量材料:测倾器、皮尺.请你根据你所掌握的知识,选择恰当的条件求出塔高.(精确到1)
小明在楼顶上看到对面山上有一座铁塔.他现有的测量材料:测倾器、皮尺.请你根据你所掌握的知识,选择恰当的条件求出塔高.(精确到1)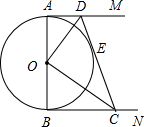 如图,AB是⊙O的直径,AM、BN是⊙O的切线,DE切⊙O于E,交AM于D,交BN于C.
如图,AB是⊙O的直径,AM、BN是⊙O的切线,DE切⊙O于E,交AM于D,交BN于C.