题目内容
14．解不等式组：$\left\{\begin{array}{l}{2x+1＞5}\\{x+1＞4（x-2）}\end{array}\right.$．分析 分别求出各不等式的解集，再求出其公共解集即可．
解答 解：$\left\{\begin{array}{l}{2x+1＞5①}\\{x+1＞4（x-2）②}\end{array}\right.$
解不等式①得：x＞2，
解不等式②得：x＜3，
所以不等式组的解集是2＜x＜3．
点评 本题考查的是解一元一次不等式组，熟知“同大取较大，同小取较小，小大大小中间找，大大小小解不了”的原则是解答此题的关键．
练习册系列答案
相关题目
4．
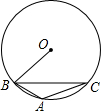如图，△ABC内接于⊙O，∠OBC=40°，则∠A的度数为（ ）
如图，△ABC内接于⊙O，∠OBC=40°，则∠A的度数为（ ）| A． | 80° | B． | 100° | C． | 110° | D． | 130° |
5．一个多边形的内角和是360°，这个多边形是（ ）
| A． | 三角形 | B． | 四边形 | C． | 六边形 | D． | 不能确定 |
2．某校要从四名学生中选拔一名参加市“风华小主播”大赛，选拔赛中每名学生的平均成绩$\overline{x}$及其方差s2如表所示，如果要选择一名成绩高且发挥稳定的学生参赛，则应选择的学生是（ ）
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8 | 9 | 9 | 8 |
| s2 | 1 | 1 | 1.2 | 1.3 |
| A． | 甲 | B． | 乙 | C． | 丙 | D． | 丁 |
6．
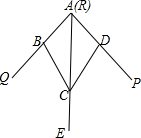如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是（ ）
如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是（ ）| A． | SAS | B． | ASA | C． | AAS | D． | SSS |
8．在?ABCD中，对角线AC和BD相交于点O，如果AC=24，BD=20，AB=m，则m的取值范围是（ ）
| A． | 20＜m＜24 | B． | 4＜m＜44 | C． | 2＜m＜22 | D． | 10＜m＜12 |
9．已知a=2-$\sqrt{3}$，b=$\sqrt{3}+2$，则a、b的关系为（ ）
| A． | 相等 | B． | 互为相反数 | C． | 互为倒数 | D． | 互为负倒数 |