题目内容
11.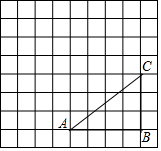 如图,每个小方格都是边长为1的正方形,△ABC为格点三角形(顶点都是格点).
如图,每个小方格都是边长为1的正方形,△ABC为格点三角形(顶点都是格点).(1)画出△ABC绕点A逆时针旋转90°后的△AB1C1;
(2)求出点C旋转到点C1经过的路径的长度(结果保留π)
分析 (1)直接利用旋转的性质分别得出B,C点对应点位置进而得出答案;
(2)直接利用旋转的性质结合弧长公式计算方法得出答案.
解答  解:(1)如图所示:△AB1C1,即为所求;
解:(1)如图所示:△AB1C1,即为所求;
(2)由条件知,AB=4,BC=3,
根据勾股定理,得
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
故l=$\frac{nπR}{180}$=$\frac{90×π×5}{180}$=$\frac{5}{2}$π,
即点C旋转到点C1经过的路径的长度为:$\frac{5}{2}$π.
点评 此题主要考查了旋转变换以及弧长计算公式应用,正确得出对应点位置是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列各式中,计算结果是负数的是( )
| A. | (-1)×(-2)×(-3)×0 | B. | 5×(-0.5)÷(-0.21) | C. | (-5)×|-3.25|×(-0.2) | D. | -(-3)2+(-2)2 |
6.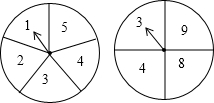 如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在偶数上的概率是( )
如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在偶数上的概率是( )
 如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在偶数上的概率是( )
如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在偶数上的概率是( )| A. | $\frac{3}{20}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
3.在平行四边形ABCD中,∠A:∠B:∠C=3:5:3,则∠D的度数是( )
| A. | 67.5° | B. | 90° | C. | 112.5° | D. | 120° |
20.据统计2016年约有1770000人参加研究生考试,把1770000用科学记数法表示为( )
| A. | 177×104 | B. | 17.7×105 | C. | 1.77×106 | D. | 0.177×107 |
 如图所示,在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=13,CD=12,求四边形ABCD的面积.
如图所示,在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=13,CD=12,求四边形ABCD的面积.