题目内容
4.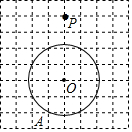 如图,网格中小正方形边长为1,点A、O、P均为格点,⊙O过点A,请过点P做⊙O的一条切线PM,切⊙O于M
如图,网格中小正方形边长为1,点A、O、P均为格点,⊙O过点A,请过点P做⊙O的一条切线PM,切⊙O于M(1)求切线PM的长为$\sqrt{13}$.
(2)描述PM的作法以OP为直径作圆交⊙O于M.
分析 (1)利用勾股定理求解;
(2)以OP为直径作圆交⊙O于M,利用圆周角定理得到∠PMO=90°.从而得到PM⊥OM.
解答 解:(1)PM=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$.
(2)以OP为直径作圆交⊙O于M,则AM为⊙O的切线.
故答案为$\sqrt{13}$;以OP为直径作圆交⊙O于M.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
14.某市今年第一季度快递业务总量达到4210000件,4210000这个数字用科学记数法表示为( )
| A. | 0.421×107 | B. | 4.21×106 | C. | 4.21×107 | D. | 4.21×104 |
19.下列调查中,不适合采用抽样调查的是( )
| A. | 了解江阴市中小学生的睡眠时间 | |
| B. | 了解无锡市初中生的兴趣爱好 | |
| C. | 了解江苏省中学教师的健康状况 | |
| D. | 了解“天宫二号”飞行器各零部件的质量 |
9.设点A(x1,y1)和B(x2,y2)是反比例函数y=$\frac{k}{x}$图象上的两个点,当x1<x2<0时,y1<y2,则一次函数y=-2x+k的图象经过( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第一、三、四象限 | D. | 第二、三、四象限 |
14.宁波奥林匹克体育中心坐落于江北区,一期“三馆一圆”总投资35亿元,其中35亿元用科学记数法表示为( )
| A. | 0.35×1010元 | B. | 3.5×108元 | C. | 3.5×109元 | D. | 35×108元 |
 如图,在一块土地上的A,B,C,D四处各有一棵树,
如图,在一块土地上的A,B,C,D四处各有一棵树, 用4个完全相同的小正方体组合成如图所示的立体图形,它的左视图为( )
用4个完全相同的小正方体组合成如图所示的立体图形,它的左视图为( )



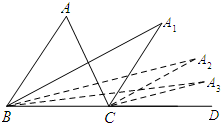 如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2013为$\frac{α}{{2}^{2012}}$.
如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2013为$\frac{α}{{2}^{2012}}$.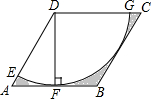 如图,在菱形ABCD中,∠DAB=60°,AD=6,DF⊥AB,以点D为圆心,DF为半径作圆弧,分别交AD,CD于点E,G,则图中阴影部分的面积为18$\sqrt{3}$-9π(结果保留π)
如图,在菱形ABCD中,∠DAB=60°,AD=6,DF⊥AB,以点D为圆心,DF为半径作圆弧,分别交AD,CD于点E,G,则图中阴影部分的面积为18$\sqrt{3}$-9π(结果保留π)