Question

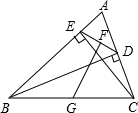
如图，在△ABC中，∠B、∠C的平分线BE，CD相交于点F，∠ABC=42°，∠A=60°，则∠BFC=(     )

A．118°  B．119°  C．120°  D．121°

Answer 1

C【考点】三角形内角和定理．

【分析】由三角形内角和定理得∠ABC+∠ACB=120°，由角平分线的性质得∠CBE+∠BCD=60°，再利用三角形的内角和定理得结果．

【解答】解：∵∠A=60°，

∴∠ABC+∠ACB=120°，

∵BE，CD是∠B、∠C的平分线，

∴∠CBE=∠ABC，∠BCD=，

∴∠CBE+∠BCD=（∠ABC+∠BCA）=60°，

∴∠BFC=180°﹣60°=120°，

故选：C．

【点评】本题主要考查了三角形内角和定理和角平分线的性质，综合运用三角形内角和定理和角平分线的性质是解答此题的关键．