题目内容
7. 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.
已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.(1)求证:AE与⊙O相切;
(2)连接BD,若ED:DO=3:1,OA=9,求AE的长;
(3)若AB=10,AC=8,点F是⊙O任意一点,点M是弦AF的中点,当点F在⊙O上运动一周,则点M运动的路径长为5π.
分析 (1)只要证明△OEC≌△OEA,得∠OAE=∠OCE=90°,即可证明.
(2)设OD=a,则DE=3a,由△OAD∽△OEA,得$\frac{OA}{OE}$=$\frac{OD}{OA}$,列出方程求出a,再利用勾股定理即可解决问题.
(3)如图2中,连接OM,取OA的中点O′,连接O′M,当点F在⊙O上运动一周,则点M运动的路径是以O′为圆心2为半径的圆,由此即可解决问题.
解答 (1)证明:如图1中,连接OC.
∵OD⊥AC,
∴AD=DC,
∴EA=EC,
在△OEC和△OEA中,
$\left\{\begin{array}{l}{OE=OE}\\{OC=OA}\\{EA=EC}\end{array}\right.$,
∴△OEC≌△OEA,
∴∠OAE=∠OCE,
∵EC是⊙O切线,
∴EC⊥OC,
∴∠OCE=90°,
∴∠OAE=∠OCE=90°,
∴OA⊥AE,
∴AE是⊙O的切线.
(2)如图1中,设OD=a,则DE=3a,
∵∠AOD=∠AOE,∠ODA=∠OAE,
∴△OAD∽△OEA,
∴$\frac{OA}{OE}$=$\frac{OD}{OA}$,
∴4a2=81,
∵a>0,
∴a=$\frac{9}{2}$,
∴OE=18,
在Rt△AOE中,AE=$\sqrt{O{E}^{2}-O{A}^{2}}$=$\sqrt{1{8}^{2}-{9}^{2}}$=9$\sqrt{3}$.
(3)如图2中,连接OM,取OA的中点O′,连接O′M.
∵AM=MF,
∴OM⊥AF,
∵AO′=OO′,OA=OB=5,
∴O′M=$\frac{1}{2}$OA=定长=$\frac{5}{2}$,
∴当点F在⊙O上运动一周,则点M运动的路径是以O′为圆心$\frac{5}{2}$为半径的圆,
∴点M运动的路径长为2π•$\frac{5}{2}$=5π.
故答案为5π.
点评 本题考查圆综合题、垂径定理、全等三角形的判定和性质、相似三角形的判定和性质、轨迹等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

| A. | 1 | B. | -196 | C. | 49 | D. | -49 |
①$y=\frac{4}{x}$,②$y=-\frac{1}{2x}$,③y=1-x,④xy=1,⑤y=2x-1,⑥$y=\frac{2}{x+1}$.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,已知∠ABC=∠DCE=90°,AC⊥DE,则图中共有相似三角形的对数为( )
如图,已知∠ABC=∠DCE=90°,AC⊥DE,则图中共有相似三角形的对数为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
| A. | 0 | B. | -π | C. | $-\sqrt{3}$ | D. | -3.14 |
| A. | -x2-4y2 | B. | 9x2+4y2 | C. | -x2+4y2 | D. | x2+(-2y)2 |
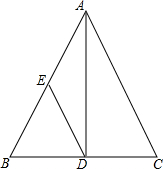 已知:如图,在△ABC中.AB=AC.点E是AB上一点.DE=AE,且DE∥AC.求证:AD是BC边上的中线.
已知:如图,在△ABC中.AB=AC.点E是AB上一点.DE=AE,且DE∥AC.求证:AD是BC边上的中线.