Question

【题目】如图，为的直径，为上一点，连接，过作于点，过点作，其中交的延长线于点．

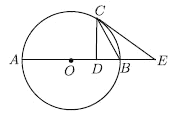
（1）求证：是的切线．

（2）如图，点在上，且满足，连接并延长交的延长线于点．

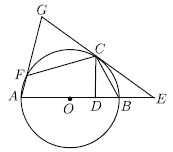
①试探究线段与之间满足的数量关系．

②若，，求线段的长．

Answer 1

【答案】（1）见解析；（2）①线段与之间满足的数量关系是：，理由见解析；②．

【解析】

（1）连接，由半径相等可得，由垂直的定义可得，继而结合已知可得，问题得证；

（2）①线段与之间满足的数量关系是：，理由如下：如图，过作于点，则有，进而通过证明，则可得，继而可得；

②在Rt△BCD中，利用勾股定理求出BC的长，再由已知可得CF的长，设，则，在中，利用勾股定理可求出OB的长，进而证明，根据相似三角形的性质即可求得答案．

（1）连接，

∵，

∴，

∵，

∴，

∵，

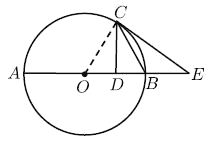
∴，即，

∴是的切线．

（2）①线段与之间满足的数量关系是：，理由如下：

如图，过作于点，

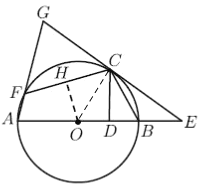
∵OH过圆心O，

∴，

∵，∠ABC=∠OCB，

∴∠OCH+∠BCE=∠FCE-∠OCB=∠OCB，

又∵∠OCB=∠OCD+∠BCD，，

∴，

∵为公共边，∠OHC=∠ODC=90°，

∴（），

∴，

∴；

②在Rt△BCD中，∠BDC=90°，BD=2，CD=4，

∴，

由①得：，

设，则，

在中，，

∴，

解得：，即，

∵，

∴

∵，，

∴，

∵四边形为的内接四边形，

∴

∴，

∴，

∴，

∴．