题目内容
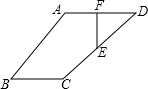
如图,已知,四边形ABCD为梯形,分别过点A、D作底边BC的垂线,垂足分别为点E、F.四边形ADFE是何种特殊的四边形?请写出你的理由.
【答案】分析:根据题意可得AD∥EF,结合AE、DF分别是底边的垂线可得∠AEF=∠DFE=90°,从而判断出AE∥DF,再结合∠AEF=90°即可作出判断.
解答:四边形ADFE是矩形.
证明:∵四边形ABCD为梯形,
∴AD∥EF.
因为AE是底边BC的垂线,所以∠AEF=90°.
同理,∠DFE=90°.
∴AE∥DF,
∴四边形ADFE为平行四边形.
又∵∠AEF=90°,
∴四边形ADFE是矩形.
点评:本题考查梯形及矩形的判定,比较简单,除此之外本题还可以根据四个角都为90°来判断四边形ADFE是矩形.
解答:四边形ADFE是矩形.
证明:∵四边形ABCD为梯形,
∴AD∥EF.
因为AE是底边BC的垂线,所以∠AEF=90°.
同理,∠DFE=90°.
∴AE∥DF,
∴四边形ADFE为平行四边形.
又∵∠AEF=90°,
∴四边形ADFE是矩形.
点评:本题考查梯形及矩形的判定,比较简单,除此之外本题还可以根据四个角都为90°来判断四边形ADFE是矩形.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1:
如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1: 如图,已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上,又点A、B分别在y轴和x轴上,∠ABO=45°.图象顶点的横坐标为2,求二次函数解析式.
如图,已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上,又点A、B分别在y轴和x轴上,∠ABO=45°.图象顶点的横坐标为2,求二次函数解析式. 如图,已知:四边形ABCD中,AD=BC,E、F分别是DC、AB的中点,直线EF分别与BC、AD的延长线相交于G、H.求证:∠AHF=∠BGF.
如图,已知:四边形ABCD中,AD=BC,E、F分别是DC、AB的中点,直线EF分别与BC、AD的延长线相交于G、H.求证:∠AHF=∠BGF.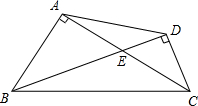 (2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25.
(2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25. 如图,已知平行四边形ABCD,点E是AD边上的点,且AE=2ED,连接BE并延长交CD的延长线于点F,
如图,已知平行四边形ABCD,点E是AD边上的点,且AE=2ED,连接BE并延长交CD的延长线于点F,